题目内容
10.已知x1,x2,x3,x4的方差是a,则3x1-5,3x2-5,3x3-5,3x4-5的方差是9a.分析 根据平均数公式与方差公式即可求解.
解答 解:设据x1,x2,x3,x4,的平均数是m,
∴$\frac{1}{4}$(x1+x2+x3+x4)=m,
∵数据x1,x2,x3,x4的平均数是m,方差是a,
∴$\frac{1}{4}$[(x1-m)2+(x2-m)2+[(x3-m)2+(x4-m)2]=a①;
∴3x1-5,3x2-5,3x3-5,3x4-5的平均数是
$\frac{1}{4}$(3x1-5+3x2-5+3x3-5+3x4-5),
=3×$\frac{1}{4}$(x1+x2+x3+x4)-5=3m-5.
∴$\frac{1}{4}$[(3x1-5-3m+5)2+(3x2-5-3m+5)2+(3x3-5-3m+5)2+(3x4-5-3m+5)2]
=$\frac{1}{4}$[9(x1-m)2+9(x2-m)2+9(x3-m)2+9(x4-m)2]②
把①代入②得,方差是:9a.
故答案为:9a
点评 本题考查了方差的知识,说明了当数据都加上一个数(或减去一个数)时,平均数也加或减这个数,方差不变,即数据的波动情况不变;当数据都乘以一个数(或除以一个数)时,平均数也乘以或除以这个数,方差变为这个数的平方倍.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
15.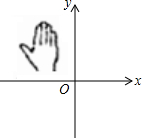 如图,小手盖住的点的坐标可能为( )
如图,小手盖住的点的坐标可能为( )
 如图,小手盖住的点的坐标可能为( )
如图,小手盖住的点的坐标可能为( )| A. | (-4,-6) | B. | (-6,3) | C. | (5,2) | D. | (3,-4) |
17.等腰三角形的一个内角是50度,它的一腰上的高与底边的夹角是( )度.
| A. | 25或10 | B. | 40或10 | C. | 25或40 | D. | 60 |
 如图,将一副直角三角板的直角顶点重叠在一起,如果∠1=28°,那么∠2=28度.
如图,将一副直角三角板的直角顶点重叠在一起,如果∠1=28°,那么∠2=28度.