题目内容
在一大片空地上有一堵墙(线段AB),现有铁栏杆40m,准备充分利用这堵墙建造一个封闭的矩形花圃,如果墙AB=8m,那么设计的花圃面积最大为
- A.100m2
- B.128m2
- C.144m2
- D.200m2
B
分析:设垂直于墙的一边的长为未知数,得到平行于墙的一边长,表示出花圃的面积,利用二次函数的最值问题及实际情况得到最大面积即可.
解答:设垂直于墙的一边的长为xm,则平行于墙的一边长为(40-2x)m,花圃的面积为y.
y=x(40-2x)
当x=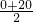 =10时,y最大,但此时40-2x=20>8,
=10时,y最大,但此时40-2x=20>8,
∴当40-2x=8时,面积最大,即x=16时,面积最大为16×8=128m2.
故选B.
点评:考查二次函数的应用;注意在使用二次函数的最值问题时也要考虑实际情况进行求解.
分析:设垂直于墙的一边的长为未知数,得到平行于墙的一边长,表示出花圃的面积,利用二次函数的最值问题及实际情况得到最大面积即可.
解答:设垂直于墙的一边的长为xm,则平行于墙的一边长为(40-2x)m,花圃的面积为y.
y=x(40-2x)
当x=
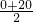 =10时,y最大,但此时40-2x=20>8,
=10时,y最大,但此时40-2x=20>8,∴当40-2x=8时,面积最大,即x=16时,面积最大为16×8=128m2.
故选B.
点评:考查二次函数的应用;注意在使用二次函数的最值问题时也要考虑实际情况进行求解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 的矩形花圃.
的矩形花圃. 的矩形花圃.
的矩形花圃.
