题目内容
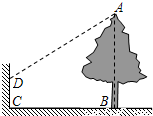
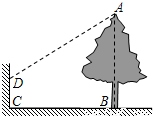
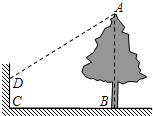 小亮想利用太阳光下的影子测量校园内一棵大树的高,小亮发现因大树靠近学校围墙,大树的影子不全落在地面上,如图所示,经测量,墙上影高CD=1.5m,地面影长BC=10m.
小亮想利用太阳光下的影子测量校园内一棵大树的高,小亮发现因大树靠近学校围墙,大树的影子不全落在地面上,如图所示,经测量,墙上影高CD=1.5m,地面影长BC=10m.(1)如果图中没有围墙,请你在图中画出大树在地面上的影子;
(2)若此时1米高的标杆的影长恰好为2m.请你求出这棵大树AB的高度.
分析:(1)延长AD交BC的延长线于点E,则BE即为大树AB的影长;
(2)过点D作DF⊥AB于点F,则CD=BF,设大树AB的高为x,则
=
,故可得出AB的高度.
(2)过点D作DF⊥AB于点F,则CD=BF,设大树AB的高为x,则
| 1 |
| 2 |
| AB-BF |
| BC |
解答:解:(1)如图1所示;
(2)过点D作DF⊥AB于点F,
∵CD⊥BC,AB⊥BC,DF⊥AB,
∴CD=BF=1.5m,
设大树AB的高为x,则
=
,
=
,解得x=6.5,
答:大树的高度是6.5m.

(2)过点D作DF⊥AB于点F,
∵CD⊥BC,AB⊥BC,DF⊥AB,
∴CD=BF=1.5m,
设大树AB的高为x,则
| 1 |
| 2 |
| AB-BF |
| BC |
| 1 |
| 2 |
| x-1.5 |
| 10 |
答:大树的高度是6.5m.

点评:本题考查的是解直角三角形的应用,熟知同一时刻物高与影长成正比是解答此题的关键.

练习册系列答案
相关题目
 小亮想利用太阳光下的影子测量校园内一棵大树的高,小亮发现因大树靠近学校围墙,大树的影子不全落在地面上,如图所示,经测量,墙上影高CD=1.5m,地面影长BC=10m.
小亮想利用太阳光下的影子测量校园内一棵大树的高,小亮发现因大树靠近学校围墙,大树的影子不全落在地面上,如图所示,经测量,墙上影高CD=1.5m,地面影长BC=10m.