题目内容
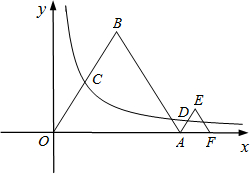
等边△OAB和△AEF的一边都在x轴上,双曲线y=
(k>0)经过边OB的中点C和AE的中点D.已知:OA=2,则△AEF的边长为______.
| k |
| x |

过C作CG⊥x轴,过D作DH⊥x轴,
∵△OAB为等边三角形,OA=2,C为OB的中点,
∴∠BOA=60°,OC=1,
在Rt△OCG中,sin∠BOA=
,cos∠BOA=
,
∴CG=OC•sin∠BOA=
,OG=OC•cos∠BOA=
,
∴C(
,
),
将C坐标代入反比例解析式中得:k=
,
∴反比例解析式为y=
,
设等边△AEF的边长为a,
∵△AEF为等边三角形,AE=AF=EF=a,C为OB的中点,
∴∠EAF=60°,AD=
a,
同理得到AH=
a,DH=
a,
∴OH=OA+AH=2+
a,
∴D(2+
a,
a),
代入反比例函数解析式得:
a(2+
a)=
,即a(2+
a)=1,
整理得:8a+a2=4,即a2+8a-4=0,
解得:a=
=-4±2
,
而a=-4-2
不合题意,舍去,故a=-4+2
,
则等边△AEF的边长为-4+2
.
故答案为:-4+2
.
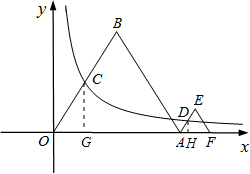
∵△OAB为等边三角形,OA=2,C为OB的中点,
∴∠BOA=60°,OC=1,
在Rt△OCG中,sin∠BOA=
| CG |
| OC |
| OG |
| OC |
∴CG=OC•sin∠BOA=
| ||
| 2 |
| 1 |
| 2 |
∴C(
| 1 |
| 2 |
| ||
| 2 |
将C坐标代入反比例解析式中得:k=
| ||
| 4 |
∴反比例解析式为y=
| ||
| 4x |
设等边△AEF的边长为a,
∵△AEF为等边三角形,AE=AF=EF=a,C为OB的中点,
∴∠EAF=60°,AD=
| 1 |
| 2 |
同理得到AH=
| 1 |
| 4 |
| ||
| 4 |
∴OH=OA+AH=2+
| 1 |
| 4 |
∴D(2+
| 1 |
| 4 |
| ||
| 4 |
代入反比例函数解析式得:
| ||
| 4 |
| 1 |
| 4 |
| ||
| 4 |
| 1 |
| 4 |
整理得:8a+a2=4,即a2+8a-4=0,
解得:a=
-8±4
| ||
| 2 |
| 5 |
而a=-4-2
| 5 |
| 5 |
则等边△AEF的边长为-4+2
| 5 |
故答案为:-4+2
| 5 |


练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目


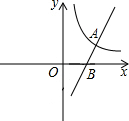

 函数,其函数图象如图所示.
函数,其函数图象如图所示. 取值范围.
取值范围.