Question

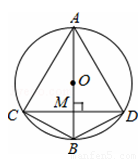
如图，AB是⊙O的直径，弦CD⊥AB，垂足为M，下列结论不成立的是(      )

A．CM=DM　     　B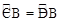．       C．∠ACD=∠ADC　   　D．OM=BM

 

Answer 1

【答案】

D.

【解析】

试题分析：∵AB是⊙O的直径，弦CD⊥AB，垂足为M，∴M为CD的中点，即CM=DM，选项A成立；

∵B为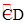的中点，即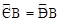，选项B成立；

在△ACM和△ADM中，∵AM=AM，∠AMC=∠AMD=90°，CM=DM，

∴△ACM≌△ADM（SAS），∴∠ACD=∠ADC，选项C成立；

而OM与BM不一定相等，选项D不成立.

故选D.

考点：1.垂径定理；2.弦、弧和圆心角的关系；3.全等三角形的判定和性质.