题目内容
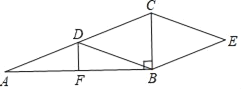
【题目】我们定义：如图1，在
中，把AB绕点
按顺时针方向旋转
得到
，把AC绕点按逆时针方向旋转
得到
，连接
.当
时，我们称
是的“旋补三角形”，边上的中线AD叫做的“旋补中线”，点A叫做“旋补中心”．
特例感知
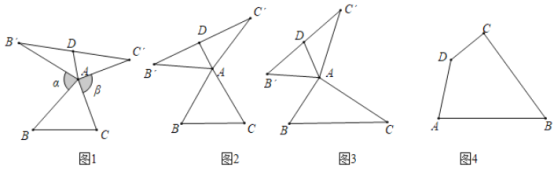
（1）在图2、图3中，
是△ABC的“旋补三角形”，
是的“旋补中线”．
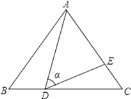
①如图2，当为等边三角形时，AD与
的数量关系为AD= ；
②如图3，当
时，则长为 ．
猜想论证
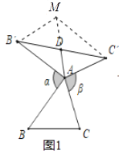
(2)在图1中，当为任意三角形时，猜想与BC的数量关系，并给予证明．
拓展应用
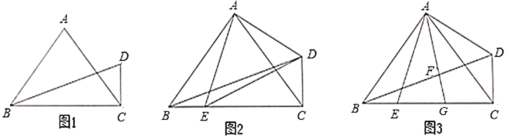
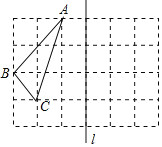
(3)如图4，在四边形
中，
.在四边形内部是否存在点
，使
是
的“旋补三角形”?若存在，求的“旋补中线”长；若不存在，说明理由．
【答案】（1）①
；②4 ；（2），证明见解析；（3）存在，
【解析】
（1）①首先证明
是含有30°的直角三角形，可得
即可解决问题；
②首先证明
，根据直角三角形斜边上的中线的性质即可解决问题；
（2）如图所示作出辅助线，首先证明四边形
是平行四边形，再证明
，即可解决问题；
（3）如图所示作出辅助线，证明PA=PD，PB=PC，再证明∠APD+∠BPC=180°即可．
解：（1）①在图2中，
∵△ABC是等边三角形，
∴AB=BC=AC=
，
∵
，
∴AD⊥
，
∵∠BAC=60°，∠BAC+
，
∴
，
∴
，
∴
，
故答案为：；
②在图3中，
∵∠BAC=90°，∠BAC+，
∴
，
∵
，
，
∴，
∴
，
∵
∴
，
故答案为：4；
（2）结论为：
理由：如下图，延长AD到点M，使得AD=DM，连接
，
，
∵，AD=DM，
∴四边形是平行四边形，
∴
，
∵∠BAC+，
∴
，
∵
∴（SAS）
∴BC=AM
∴；
（3）存在，
理由：如图4中，延长AD交BC的延长线于点M，作BE⊥AD于点E，作线段BC的垂直平分线交BE于点P，交BC于点F，连接PA、PD、PC，作△PCD的中线PN，连接DF交PC于点O．
∵∠ADC=150°，
∴∠MDC=30°，
在Rt△DCM中，
∵
，∠DCM=90°，∠MDC=30°，
∴CM=2，DM=4，∠M=60°，
在Rt△BEM中，∵∠BEM=90°，BM=14，∠MBE=30°，
∴EM=
，
∴DE=EM-DM=3，
∵AD=6，
∴AE=DE，
∵BE⊥AD，
∴PA=PD，PB=PC，
在Rt△CDF中，∵CD=
，CF=6，
∴
，
∴∠CDF=60°=∠CPF，
∴△FCP≌△CFD，
∴CD=PF，
又∵CD∥PF
∴四边形CDPF是矩形，
∴∠CDP=90°，
∴∠ADP=∠ADC-∠CDP=60°，
∴△ADP是等边三角形，
∴∠ADP=60°，
∵∠BPF=∠CPF=60°，
∴∠BPC=120°，
∴∠APD+∠BPC=180°，
∴△PCD是△PAB的“旋补三角形”，
在Rt△PDN中，∵∠PDN=90°，PD=AD=6，DN=
，
PN=
．
