题目内容
【题目】背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五.它被记载于我国古代著名数学著作《周髀算经》中,在本题中,我们把三边的比为3∶4∶5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
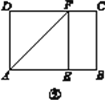
实践操作 如图①,在矩形纸片ABCD中,AD=8 cm,AB=12 cm.
第一步:如图②,将图①中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图③,将图②中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
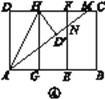
第三步:如图④,将图③中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.
问题解决
(1)请在图②中证明四边形AEFD是正方形;
(2)请在图④中判断NF与ND′的数量关系,并加以证明;
(3)请在图④中证明△AEN是(3,4,5)型三角形.


【答案】(1)证明见解析(2)NF=ND′(3)证明见解析
【解析】
(1)根据矩形的性质得到∠D=∠DAE=90°,由折叠的性质得得到AE=AD,∠AEF=∠D=90°,求得∠D=∠DAE=∠AEF=90°,得到四边形AEFD是矩形,由于AE=AD,于是得到结论;
(2)连接HN,由折叠的性质得到∠AD′H=∠D=90°,HF=HD=HD′,根据正方形的想知道的∠HD′N=90°,根据全等三角形的性质即可得到结论;
(3)根据正方形的性质得到AE=EF=AD=8cm,由折叠得,AD′=AD=8cm,设NF=xcm,则ND′=xcm,根据勾股定理列方程得到x=2,于是得到结论;
(1)证明:∵四边形ABCD是矩形,
∴∠D=∠DAE=90°.
由折叠的性质得AE=AD,∠AEF=∠D=90°,∴∠D=∠DAE=∠AEF=90°,
∴四边形AEFD是矩形.
又∵AE=AD,∴矩形AEFD是正方形.
(2)NF=ND′.
证明:连接HN,由折叠的性质得∠AD′H=∠D=90°,HF=HD=HD′.
由(1)知四边形AEFD是正方形,∴∠EFD=90°.
∵∠AD′H=90°,∴∠HD′N=90°.
在Rt△HNF和Rt△HND′中,
∵HN=HN,HF=HD′,
∴Rt△HNF≌Rt△HND′,
∴NF=ND′.
(3)证明:由(1)知四边形AEFD是正方形,
∴AE=EF=AD=8 cm,
由折叠的性质得AD′=AD=8 cm.
设NF=x cm,则ND′=x cm.
在Rt△AEN中,∵AN2=AE2+EN2,∴(8+x)2=82+(8-x)2,解得x=2,∴AN=8+x=10 cm,EN=6 cm,∴EN∶AE∶AN=3∶4∶5,∴△AEN是(3,4,5)型三角形.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案