题目内容
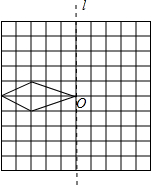 (2012•漳州)利用对称性可设计出美丽的图案.在边长为1的方格纸中,有如图所示的四边形(顶点都在格点上).
(2012•漳州)利用对称性可设计出美丽的图案.在边长为1的方格纸中,有如图所示的四边形(顶点都在格点上).(1)先作出该四边形关于直线l成轴对称的图形,再作出你所作的图形连同原四边形绕0点按顺时针方向旋转90°后的图形;
(2)完成上述设计后,整个图案的面积等于
20
20
.分析:(1)根据图形对称的性质先作出关于直线l的对称图形,再作出所作的图形连同原四边形绕0点按顺时针方向旋转90°后的图形即可;
(2)先利用割补法求出原图形的面积,由图形旋转及对称的性质可知经过旋转与轴对称所得图形与原图形全等即可得出结论.
(2)先利用割补法求出原图形的面积,由图形旋转及对称的性质可知经过旋转与轴对称所得图形与原图形全等即可得出结论.
解答: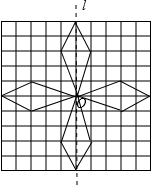 解:(1)如图所示:
解:(1)如图所示:
先作出关于直线l的对称图形;
再作出所作的图形连同原四边形绕0点按顺时针方向
旋转90°后的图形.
(2)∵边长为1的方格纸中一个方格的面积是1,
∴原图形的面积为5,
∴整个图案的面积=4×5=20.
故答案为:20.
 解:(1)如图所示:
解:(1)如图所示:先作出关于直线l的对称图形;
再作出所作的图形连同原四边形绕0点按顺时针方向
旋转90°后的图形.
(2)∵边长为1的方格纸中一个方格的面积是1,
∴原图形的面积为5,
∴整个图案的面积=4×5=20.
故答案为:20.
点评:本题考查的是利用旋转及轴对称设计图案,熟知经过旋转与轴对称所得图形与原图形全等是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
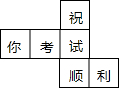 (2012•漳州)如图,是一个正方体的平面展开图,原正方体中“祝”的对面是( )
(2012•漳州)如图,是一个正方体的平面展开图,原正方体中“祝”的对面是( )