题目内容
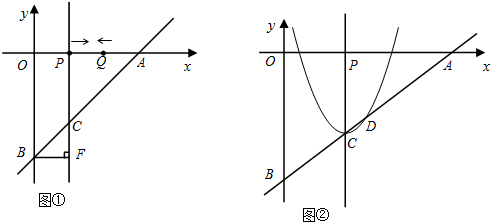
(2012•晋江市质检)已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)填空:CQ=
(2)当t为何值时,点P在以AQ为直径的⊙M上?
(3)当P、Q、F三点在同一条直线上时,如图(3),求t的值.

(1)填空:CQ=
t
t
,AQ=8-t
8-t
(用含t的式子表示);(2)当t为何值时,点P在以AQ为直径的⊙M上?
(3)当P、Q、F三点在同一条直线上时,如图(3),求t的值.

分析:(1)根据等腰直角三角形的性质得出EC=QC,进而得出AQ的长;
(2)根据相似三角形的判定得出△ABC∽△AQP,进而表示出AP,AQ,利用相似三角形的性质求出即可;
(3)首先证明△PAN∽△BAC,再得出△QCF∽△QNP,即可得出
=
,求出t的值即可.
(2)根据相似三角形的判定得出△ABC∽△AQP,进而表示出AP,AQ,利用相似三角形的性质求出即可;
(3)首先证明△PAN∽△BAC,再得出△QCF∽△QNP,即可得出
| PN |
| FC |
| NQ |
| CQ |
解答:解:(1)∵∠QCE=90°,∠DEF=45°,
∴EC=CQ,
∴CQ=t,AQ=AC-QC=8-t,
故答案为:t,8-t;
(2)若点P在AQ为直径的⊙M上,如图2,则必须有∠APQ=90°,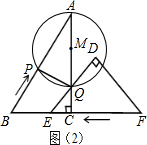
由题意得出,∠ACB=90°,
∴∠APQ=∠ACB=90°,
又∠A=∠A,
∴△ABC∽△AQP,
∴
=
,
由题意得出:BP=2t,EC=t,
在Rt△ABC中,AC=8cm,BC=6cm,
由勾股定理得出:AB=
=10(cm),
∴AP=10-2t由(1)得:
AQ=8-t,
∴
=
,
解得:t=3,
∴当t=3s时,点P在以AQ为直径的⊙M上,
(3)当点P、Q、F三点在同一直线上时,如图3,过P作PN⊥AC于点N,
∴∠ANP=∠ACB=∠PNQ=90°,
∵∠PAN=∠BAC,
∴△PAN∽△BAC,
∴
=
=
,
∴
=
=
,
∴PN=6-
t,
AN=8-
t,
∵NQ=AQ-AN,
∴NQ=8-t-(8-
t)=
t,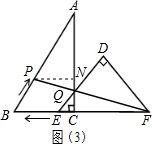
∵∠ACB=90°,
∵点B、C(E)、F三点在同一直线上,
∴∠QCF=90°,∠QCF=∠PNQ,
∵∠FQC=∠PQN,
∴△QCF∽△QNP,
∴
=
,
∴
=
,
∵0<t<4.5,
∴
=
,
解得:t=1.
∴EC=CQ,
∴CQ=t,AQ=AC-QC=8-t,
故答案为:t,8-t;
(2)若点P在AQ为直径的⊙M上,如图2,则必须有∠APQ=90°,

由题意得出,∠ACB=90°,
∴∠APQ=∠ACB=90°,
又∠A=∠A,
∴△ABC∽△AQP,
∴
| AP |
| AC |
| AQ |
| AB |
由题意得出:BP=2t,EC=t,
在Rt△ABC中,AC=8cm,BC=6cm,
由勾股定理得出:AB=
| AC2+BC2 |
∴AP=10-2t由(1)得:
AQ=8-t,
∴
| 10-2t |
| 8 |
| 8-t |
| 10 |
解得:t=3,
∴当t=3s时,点P在以AQ为直径的⊙M上,
(3)当点P、Q、F三点在同一直线上时,如图3,过P作PN⊥AC于点N,
∴∠ANP=∠ACB=∠PNQ=90°,
∵∠PAN=∠BAC,
∴△PAN∽△BAC,
∴
| PN |
| BC |
| AP |
| AB |
| AN |
| AC |
∴
| PN |
| 6 |
| 10-2t |
| 10 |
| AN |
| 8 |
∴PN=6-
| 6 |
| 5 |
AN=8-
| 8 |
| 5 |
∵NQ=AQ-AN,
∴NQ=8-t-(8-
| 8 |
| 5 |
| 3 |
| 5 |

∵∠ACB=90°,
∵点B、C(E)、F三点在同一直线上,
∴∠QCF=90°,∠QCF=∠PNQ,
∵∠FQC=∠PQN,
∴△QCF∽△QNP,
∴
| PN |
| FC |
| NQ |
| CQ |
∴
6-
| ||
| 9-t |
| ||
| t |
∵0<t<4.5,
∴
6-
| ||
| 9-t |
| 3 |
| 5 |
解得:t=1.
点评:此题主要考查了相似三角形的判定与性质以及勾股定理的应用等知识,正确利用相似三角形的性质得出PN,AN的长度是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目