题目内容
已知△ABC是非等腰直角三角形，∠BAC=90°，在BC所在直线上取两点D、E，使BD=BC=CE，连接AD、AE；已知∠BAD=45°，那么tan∠CAE= ．
分析：过B、C两点作BM∥AC，CN∥AB，由中位线可得AC=2BM，AB=2CN，则tan∠BAD•tan∠CAE=
，又45°角所对的正切值为1，进而即可求出结论．
| 1 |
| 4 |
解答：解：如图，过B、C两点作BM∥AC，CN∥AB分别交AD、AE于M、N，
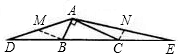
∵BD=BC，即点B为CD的中点，
∴AC=2BM，
同理AB=2CN，又tan∠BAD=
，tan∠CAE=
，从而
tan∠BAD•tan∠CAE=
，
∵tan∠BAD=1，
∴tan∠CAE=
．
故答案为
．
∵BD=BC，即点B为CD的中点，
∴AC=2BM，
同理AB=2CN，又tan∠BAD=
| BM |
| AB |
| CN |
| AC |
tan∠BAD•tan∠CAE=
| 1 |
| 4 |
∵tan∠BAD=1，
∴tan∠CAE=
| 1 |
| 4 |
故答案为
| 1 |
| 4 |
点评：本题主要考查了平行线分线段成比例的性质问题以及三角函数的一些基础知识，能够掌握并熟练运用．
练习册系列答案
阅读快车系列答案
相关题目