题目内容
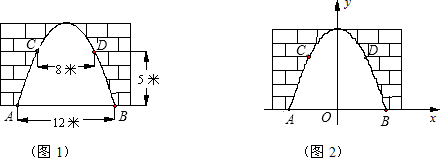
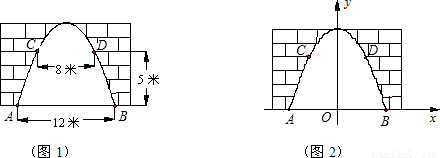
如图,某地一古城墙门洞呈抛物线形,已知门洞的地面宽度AB=12米,两侧距地面5米高C、D处各有一盏路灯,两灯间的水平距离CD=8米,求这个门洞的高度.(提示:选择适当的位置为原点建立直角坐标系,例如图:以AB的中点为坐标原点建立直角坐标系.)

解:由题意可知各点的坐标,A(-6,0),B(6,0),C(-4,5),D(4,5),
由于顶点在y轴,可设抛物线的解析式为y=ax2+c,将点A(-6,0),D(4,5)的坐标代入,
得方程组: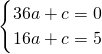 ,
,
解得: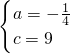 ,
,
∴抛物线的解析式为:y=- x2+9.
x2+9.
答:门洞的高度是9米.
分析:由题意可知各点的坐标,A(-6,0),B(6,0),C(-4,5),D(4,5),又由抛物线的顶点在y轴上,即可设抛物线的解析式为y=ax2+c,然后利用待定系数法即可求得此二次函数的解析式,继而求得这个门洞的高度.
点评:此题考查了二次函数在实际生活中的应用.题目难度适中,解此题的关键是理解题意,求得相应的函数解析式,注意待定系数法的应用.
由于顶点在y轴,可设抛物线的解析式为y=ax2+c,将点A(-6,0),D(4,5)的坐标代入,
得方程组:
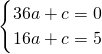 ,
,解得:
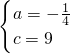 ,
,∴抛物线的解析式为:y=-
 x2+9.
x2+9.答:门洞的高度是9米.
分析:由题意可知各点的坐标,A(-6,0),B(6,0),C(-4,5),D(4,5),又由抛物线的顶点在y轴上,即可设抛物线的解析式为y=ax2+c,然后利用待定系数法即可求得此二次函数的解析式,继而求得这个门洞的高度.
点评:此题考查了二次函数在实际生活中的应用.题目难度适中,解此题的关键是理解题意,求得相应的函数解析式,注意待定系数法的应用.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目