Question

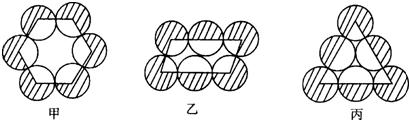
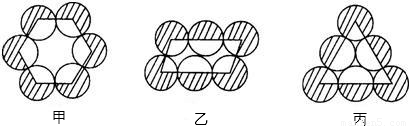
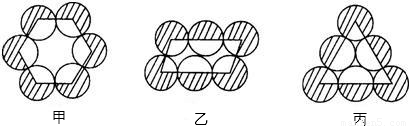
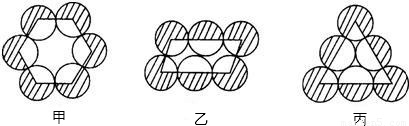
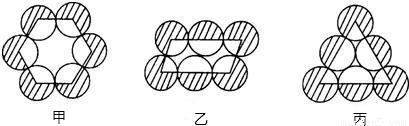
有六个等圆按甲，乙，丙三种形式摆放，使相邻两圆相互外切，如图所示，它们的连心线分别构成正六边形，平行四边形和正三角形，将圆心连线外侧的6个扇形（阴影部分）的面积之和依次记为S，P，Q，则（ ）

A．S＞P＞Q
B．S＞Q＞P
C．S＞P且S=Q
D．S=P=Q

Answer 1

【答案】分析：阴影部分的面积可以看作是六个等圆面积减去两个等圆的面积计算．
解答：解：正六边形的内角和为720°，所以内侧6个扇形的面积之和是2个等圆的面积；
平行四边形的内角和为360°，所以内侧6个扇形的面积之和也是2个等圆的面积；
正三角形的内角和为180°，所以内侧6个扇形的面积之和也是2个等圆的面积；
都是六个等圆减去2个等圆的面积，
所以将圆心连线外侧的6个扇形（阴影部分）的面积之和是相等，
故选D．
点评：求不规则的图形的面积，可以转化为几个规则图形的面积的和或差来求．