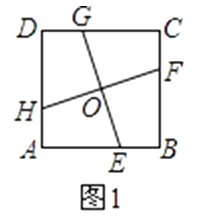
题目内容
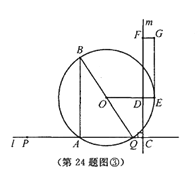
【题目】(本题14分)如图,点A和动点P在直线![]() 上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线
上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O。点C在点P右侧,PC=4,过点C作直线![]() ⊥
⊥![]() ,过点O作OD⊥
,过点O作OD⊥![]() 于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=
于点D,交AB右侧的圆弧于点E。在射线CD上取点F,使DF=![]() CD,以DE,DF为邻边作矩形DEGF,设AQ=
CD,以DE,DF为邻边作矩形DEGF,设AQ=![]()
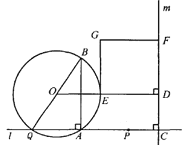
(1)用关于![]() 的代数式表示BQ,DF;
的代数式表示BQ,DF;
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长;
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于另一点N,若BN的弦心距为1,求AP的长(直接写出答案)
【答案】BQ=5x,DF=3x;AP=9;AP为12或![]() 或3时,矩形DEGF是正方形;AP的长为6
或3时,矩形DEGF是正方形;AP的长为6![]() 或
或![]() .
.
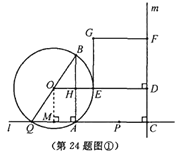
【解析】试题分析:(1)根据Rt△ABQ中AQ:AB=3:4得出AQ=3x,AB=4x,BQ=5x,根据CD⊥m,l⊥m得出OD∥l,则OB=OQ,AH=BH=2x,则CD=2x,则FD=![]() CD=3x;(2)AP=AQ=3x PC=4 ∴CQ="6x+4" 作OM⊥AQ于点M(如图①)根据外接圆的性质得出∠BAQ=90°,则点O是BQ的中点,则QM=AM=
CD=3x;(2)AP=AQ=3x PC=4 ∴CQ="6x+4" 作OM⊥AQ于点M(如图①)根据外接圆的性质得出∠BAQ=90°,则点O是BQ的中点,则QM=AM=![]() x,则OD=MC=
x,则OD=MC=![]() x+4,OE=
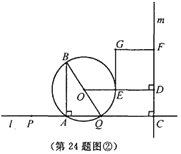
x+4,OE=![]() x,ED=2x+4,根据矩形的面积求出x的值,从而的好粗AP的长度;(3)①当矩形为正方形时,则ED=FD,点P在点A的右侧时,画出图形得出2x+4=3x,得出x的值和AP的长度;点P在点A的左侧时,当点C在点Q右侧当 0<x<
x,ED=2x+4,根据矩形的面积求出x的值,从而的好粗AP的长度;(3)①当矩形为正方形时,则ED=FD,点P在点A的右侧时,画出图形得出2x+4=3x,得出x的值和AP的长度;点P在点A的左侧时,当点C在点Q右侧当 0<x<![]() 时,画出图形得出ED=4-7x,FD=3x,求出x的值和AP的长度;当
时,画出图形得出ED=4-7x,FD=3x,求出x的值和AP的长度;当![]() ≤x<
≤x<![]() 时, ED=7-4x,DF=3x,从而求出x的值;当点C在点Q左侧时,即x≥
时, ED=7-4x,DF=3x,从而求出x的值;当点C在点Q左侧时,即x≥![]() 画出图形可得:DE=7x-4,DF=3x,然后求出x的值和AP的长度;②、连结NQ,有点O到BN的弦心距为1得:NQ=2,当点N在AB的左侧时画出图形,过点B作BM⊥EG于点M,根据GM=x,BM=x得出∠GBM=45°,根据BM∥AQ,decubitusAI="AB=4x" ,IQ=x,NQ=
画出图形可得:DE=7x-4,DF=3x,然后求出x的值和AP的长度;②、连结NQ,有点O到BN的弦心距为1得:NQ=2,当点N在AB的左侧时画出图形,过点B作BM⊥EG于点M,根据GM=x,BM=x得出∠GBM=45°,根据BM∥AQ,decubitusAI="AB=4x" ,IQ=x,NQ=![]() =2,从而求出x的值,得出AP的长度;当点N在AB的右侧时,画出图形,然后利用同样的方法求出AP的长度.
=2,从而求出x的值,得出AP的长度;当点N在AB的右侧时,画出图形,然后利用同样的方法求出AP的长度.
试题解析:(1)在Rt△ABQ中,∵AQ:AB=3:4 ∴AQ=3x ∴AB=4x BQ=5x
又∵CD⊥m,l⊥m ∴OD∥l ∵OB=OQ ∴AH=BH=![]() AB=2x ∴CD=2x ∴FD=
AB=2x ∴CD=2x ∴FD=![]() CD=3x
CD=3x
(2)∵AP=AQ=3x PC=4 ∴CQ=6x+4 作OM⊥AQ于点M(如图①) ∴OM∥AB
∵![]() O是△ABQ的外接圆 ∠BAQ=90° ∴点O是BQ的中点 ∴QM=AM=
O是△ABQ的外接圆 ∠BAQ=90° ∴点O是BQ的中点 ∴QM=AM=![]() x ∴OD=MC=
x ∴OD=MC=![]() x+4
x+4
∴OE=![]() BQ=
BQ=![]() x ∴ED=2x+4 ∴矩形DEGF的面积=DF·DE=3x(2x+4)=90
x ∴ED=2x+4 ∴矩形DEGF的面积=DF·DE=3x(2x+4)=90
∴![]() =-5(舍去)
=-5(舍去)![]() =3 ∴AP=3x=9
=3 ∴AP=3x=9
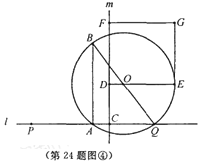
(3)①若矩形DEGF是正方形 则ED=FD
I、点P在点A的右侧时(如图①) ∴2x+4=3x,解得:x=4 ∴AP=3x=12
II、点P在点A的左侧时 当点C在点Q右侧 0<x<![]() 时(如图②) ∵ED=4-7x,FD=3x
时(如图②) ∵ED=4-7x,FD=3x
∴4-7x=3x 解得:x=![]() ∴AP=
∴AP=![]()
当![]() ≤x<
≤x<![]() 时(如图③) ED=7-4x,DF=3x ∴7-4x=3x 解得:x=1(舍去)
时(如图③) ED=7-4x,DF=3x ∴7-4x=3x 解得:x=1(舍去)
当点C在点Q左侧时,即x≥![]() (如图④) DE=7x-4 DF=3x ∴7x-4=3x 解得:x=1 ∴AP=3
(如图④) DE=7x-4 DF=3x ∴7x-4=3x 解得:x=1 ∴AP=3
综上所述:当AP为12或![]() 或3时,矩形DEGF是正方形
或3时,矩形DEGF是正方形
②、AP的长为6![]() 或
或![]()
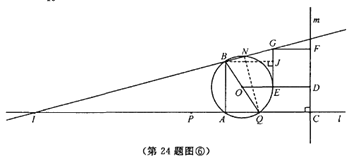
连结NQ,有点O到BN的弦心距为1得:NQ=2
当点N在AB的左侧时(如图⑤) 过点B作BM⊥EG于点M ∵GM=x,BM=x ∴∠GBM=45°
∴BM∥AQ,∴AI=AB=4x ∴IQ=x ∴NQ=![]() =2 ∴x=2
=2 ∴x=2![]() ∴AP=6
∴AP=6![]()
当点N在AB的右侧时(如图⑥),过点B作BJ⊥GE于点J ∵GJ=x,BJ=4x ∴tan∠GBJ=![]()
∴AI=16x ∴QI=19x ∴NQ=![]() =2 ∴x=
=2 ∴x=![]() ∴AP=
∴AP=![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】为了进一步了解九年级500名学生的身体素质情况,体育老师对九年级(1)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图如下所示: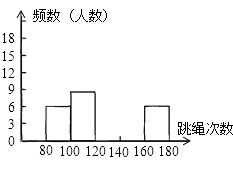
组别 | 次数x | 频数(人数) |
第l组 | 80≤x<100 | 6 |
第2组 | 100≤x<120 | 8 |
第3组 | 120≤x<140 | a |
第4组 | 140≤x<160 | 18 |
第5组 | 160≤x<180 | 6 |
请结合图表完成下列问题:
(1)表中的a=,次数在140≤x<160这组的频率为;
(2)请把频数分布直方图补充完整;
(3)若九年级学生一分钟跳绳次数(x)达标要求是:x<120不合格;x≥120为合格,则这个年级合格的学生有人.