题目内容
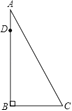
【题目】如图,AB为一棵大树,在树上距地面10米的D处有两只猴子,他们同时发现C处有一筐水果,一只猴子从D处往上爬到树顶A处,又沿滑绳AC滑到C处,另一只猴子从D滑到B,再由B跑到C处,已知两只猴子所经路程都为15米,求树高AB.
【答案】12米
【解析】分析:在Rt△ABC中,∠B=90°,则满足AB+BC=AC,BC=a(米),AC=b(米),AD=x(米),根据两只猴子经过的路程一样可得10+a=x+b=15解方程组可以求x的值,即可计算树高=10+x.
Rt△ABC中,∠B=90°,
本题解析:
设BC=a(米),AC=b(米),AD=x(米)
则10+a=x+b=15(米).
∴a=5(米),b=15x(米)
又在Rt△ABC中,由勾股定理得:(10+x)+a=b,
∴(10+x)+5=(15x),
解得,x=2,即AD=2(米)
∴AB=AD+DB=2+10=12(米)
答:树高AB为12米。

练习册系列答案
相关题目