题目内容
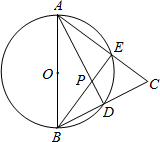（2012•肇庆）如图，在△ABC中，AB=AC，以AB为直径的⊙O交AC于点E，交BC于点D，连接BE、AD交于点P．求证：（1）D是BC的中点；
（2）△BEC∽△ADC；
（3）AB•CE=2DP•AD．
分析：（1）由AB是⊙O的直径，可得AD⊥BC，又由AB=AC，由三线合一，即可证得D是BC的中点；
（2）由AB是⊙O的直径，∠AEB=∠ADB=90°，又由∠C是公共角，即可证得△BEC∽△ADC；
（3）易证得△ABD∽△BCE与△BPD∽△BCE，根据相似三角形的对应边成比例与BC=2BD，即可证得AB•CE=2DP•AD．
（2）由AB是⊙O的直径，∠AEB=∠ADB=90°，又由∠C是公共角，即可证得△BEC∽△ADC；
（3）易证得△ABD∽△BCE与△BPD∽△BCE，根据相似三角形的对应边成比例与BC=2BD，即可证得AB•CE=2DP•AD．
解答：证明：（1）∵AB是⊙O的直径，
∴∠ADB=90°，即AD⊥BC，
∵AB=AC，
∴D是BC的中点；
（2）∵AB是⊙O的直径，
∴∠AEB=∠ADB=90°，
即∠CEB=∠CDA=90°，
∵∠C是公共角，
∴△BEC∽△ADC；
（3）∵△BEC∽△ADC，
∴∠CBE=∠CAD，
∵AB=AC，BD=CD，
∴∠BAD=∠CAD，
∴∠BAD=∠CBE，
∵∠ADB=∠BEC=90°，
∴△ABD∽△BCE，
∴
=
，
∴
=
，
∵∠BDP=∠BEC=90°，∠PBD=∠CBE，
∴△BPD∽△BCE，
∴
=
，
∵BC=2BD，∴AB：AD=2BD：BE，
∴
=
，
∴AB•CE=2DP•AD．
∴∠ADB=90°，即AD⊥BC，
∵AB=AC，
∴D是BC的中点；
（2）∵AB是⊙O的直径，
∴∠AEB=∠ADB=90°，
即∠CEB=∠CDA=90°，
∵∠C是公共角，
∴△BEC∽△ADC；
（3）∵△BEC∽△ADC，
∴∠CBE=∠CAD，
∵AB=AC，BD=CD，
∴∠BAD=∠CAD，
∴∠BAD=∠CBE，
∵∠ADB=∠BEC=90°，
∴△ABD∽△BCE，
∴
| AB |
| BC |
| AD |
| BE |
∴
| AB |
| AD |
| BC |
| BE |
∵∠BDP=∠BEC=90°，∠PBD=∠CBE，
∴△BPD∽△BCE，
∴
| DP |
| CE |
| BD |
| BE |
∵BC=2BD，∴AB：AD=2BD：BE，
∴
| AB |
| AD |
| 2DP |
| CE |
∴AB•CE=2DP•AD．
点评：此题考查了相似三角形的判定与性质、圆周角定理以及等腰三角形的性质．此题难度适中，注意数形结合思想的应用．
练习册系列答案
相关题目
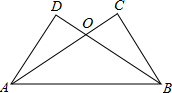（2012•肇庆）如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．
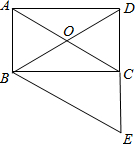（2012•肇庆）如图，四边形ABCD是矩形，对角线AC、BD相交于点O，BE∥AC交DC的延长线于点E．
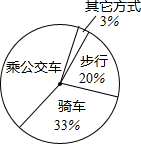（2012•肇庆一模）某中学就到校的方式问题对初三年级的所有学生进行了一次调查，并将调查结果制作了扇形统计图（如图）．已知步行人数为60人．
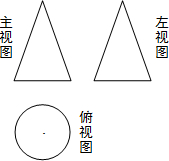（2012•肇庆）如图是某几何体的三视图，则该几何体是（ ）