题目内容
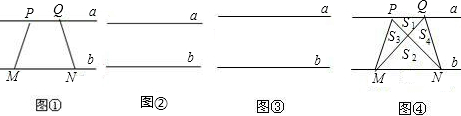
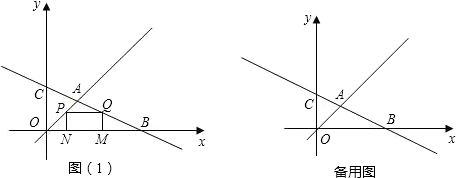
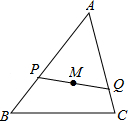 如图,线段PQ过△ABC重心M,P,Q分别内分AB,AC为比值p,q,则
如图,线段PQ过△ABC重心M,P,Q分别内分AB,AC为比值p,q,则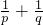 =
=
- A.2
- B.1
- C.

- D.无法确定
B
分析:根据三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.可以分别过点B,C作BE∥AD,CF∥AD,交PQ于点E,F,根据平行线等分线段定理和梯形中位线定理可得到两个等式,代入所求代数式整理即可得到答案.
解答: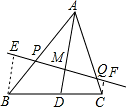 解:分别过点B,C作BE∥AD,CF∥AD,交PQ于点E,F,则ME=MF,
解:分别过点B,C作BE∥AD,CF∥AD,交PQ于点E,F,则ME=MF,
则根据梯形的中位线定理得:
∵MD是梯形的中位线,
∴BE+CF=2MD,
∴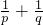 =
=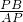 +
+ =
=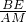 +
+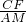 =
=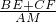 =
=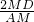 =1.
=1.
故选B.
点评:此题考查了重心的概念和性质,能够熟练运用平行线分线段成比例定理、平行线等分线段定理以及梯形的中位线定理.
分析:根据三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.可以分别过点B,C作BE∥AD,CF∥AD,交PQ于点E,F,根据平行线等分线段定理和梯形中位线定理可得到两个等式,代入所求代数式整理即可得到答案.
解答:
 解:分别过点B,C作BE∥AD,CF∥AD,交PQ于点E,F,则ME=MF,
解:分别过点B,C作BE∥AD,CF∥AD,交PQ于点E,F,则ME=MF,则根据梯形的中位线定理得:
∵MD是梯形的中位线,
∴BE+CF=2MD,
∴
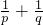 =
=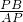 +
+ =
=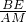 +
+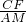 =
=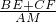 =
=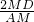 =1.
=1.故选B.
点评:此题考查了重心的概念和性质,能够熟练运用平行线分线段成比例定理、平行线等分线段定理以及梯形的中位线定理.

练习册系列答案
相关题目
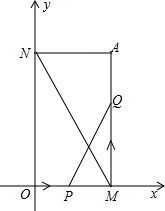 如图,已知过A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.
如图,已知过A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.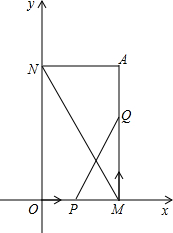 如图,已知过A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.
如图,已知过A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.