题目内容
针对下列图象李明同学说到：图①可能是y=-x2+4x；图②可能是y=（x-2）2-1；图③可能是y=-3x2-4x+1；图④可能是y=x2-4x+1
你认为其中必定正确的有（ ）
你认为其中必定正确的有（ ）
分析：分别求出各二次函数与y轴的交点坐标，顶点坐标，然后进行判断即可．
解答：解：①y=-x2+4x=-（x-2）2+4与y轴的交点坐标为（0，0），
顶点坐标为（2，4），图象正确；
图②y=（x-2）2-1顶点坐标是（2，-1），图象错误；
图③y=-3x2-4x+1=-3（x+
）2+
与y轴的交点坐标为（0，1），
顶点坐标为（-
，
），图象错误；
图④y=x2-4x+1=（x-2）2-3，与y轴的交点坐标为（0，1），
顶点坐标为（2，-3），图象正确，
所以，正确的有①④共2个．
故选B．
顶点坐标为（2，4），图象正确；
图②y=（x-2）2-1顶点坐标是（2，-1），图象错误；
图③y=-3x2-4x+1=-3（x+
| 2 |
| 3 |
| 7 |
| 3 |
顶点坐标为（-
| 2 |
| 3 |
| 7 |
| 3 |
图④y=x2-4x+1=（x-2）2-3，与y轴的交点坐标为（0，1），
顶点坐标为（2，-3），图象正确，
所以，正确的有①④共2个．
故选B．
点评：本题考查了二次函数的图象，根据函数解析式求出与y轴的交点坐标以及顶点坐标是解题的关键．
练习册系列答案
相关题目
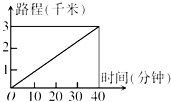如图所示，是李明从家出发步行到学校的路程与时间的关系图，根据这个图象有下列说法：①李明家距离学校3千米；②李明从家到学校用40分钟；③李明在途中没有停下来；④李明步行的平均速度为4千米/小时，在这四种说法中，正确的个数有（ ）
如图所示，是李明从家出发步行到学校的路程与时间的关系图，根据这个图象有下列说法：①李明家距离学校3千米；②李明从家到学校用40分钟；③李明在途中没有停下来；④李明步行的平均速度为4千米/小时，在这四种说法中，正确的个数有