题目内容
【题目】在平面直角坐标系中,已知![]() ,
,![]() .
.
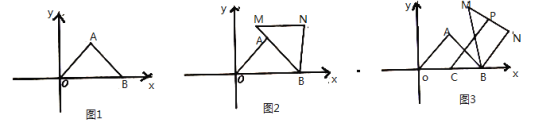
(1)如图1,求![]() 的值.
的值.
(2)把![]() 绕着点
绕着点![]() 顺时针旋转,点
顺时针旋转,点![]() 、
、![]() 旋转后对应的点分别为
旋转后对应的点分别为![]() 、
、![]() .
.
①当![]() 恰好落在
恰好落在![]() 的延长线上时,如图2,求出点
的延长线上时,如图2,求出点![]() 、
、![]() 的坐标.
的坐标.
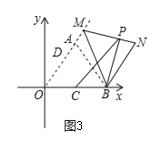
②若点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 上的动点,如图3,在旋转过程中,请直接写出线段
上的动点,如图3,在旋转过程中,请直接写出线段![]() 长的取值范围.
长的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ,②
,②![]() ;(3)
;(3)![]()
【解析】
(1)作AH⊥OB,根据正弦的定义即可求解;
(2)作MC⊥OB,先求出直线AB解析式,根据等腰三角形的性质及三角函数的定义求出M点坐标,根据MN∥OB,求出N点坐标;
(3)由于点C是定点,点P随△ABO旋转时的运动轨迹是以B为圆心,BP长为半径的圆,故根据点和圆的位置关系可知,当点P在线段OB上时,CP=BP-BC最短;当点P在线段OB延长线上时,CP=BP+BC最长.又因为BP的长因点D运动而改变,可先求BP长度的范围.由垂线段最短可知,当BP垂直MN时,BP最短,求得的BP代入CP=BP-BC求CP的最小值;由于BM>BN,所以点P与M重合时,BP=BM最长,代入CP=BP+BC求CP的最大值.
(1)作AH⊥OB,
∵![]() ,
,![]() .
.
∴H(3,5)
∴AH=3,AH=![]()
∴![]() =
=![]() =
=![]()
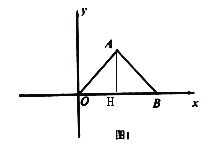
(2)由(1)得A(3,4),又![]()
求得直线AB的解析式为:y=![]()
∵旋转,∴MB=OB=6,
作MC⊥OB,∵AO=BO,
∴∠AOB=∠ABO
∴MC=MBsin∠ABO=6×![]() =
=![]()
即M点的纵坐标为![]() ,代入直线AB得x=
,代入直线AB得x=![]()
∴![]() ,
,
∵∠NMB=∠AOB=∠ABO
∴MN∥OB,又MN=AB=5,
则![]() +5=
+5=![]()
∴![]()
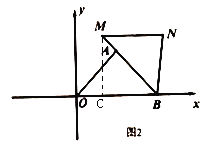
(3)连接BP
∵点D为线段OA上的动点,OA的对应边为MN
∴点P为线段MN上的动点
∴点P的运动轨迹是以B为圆心,BP长为半径的圆
∵C在OB上,且CB=![]() OB=3
OB=3
∴当点P在线段OB上时,CP=BPBC最短;当点P在线段OB延长线上时,CP=BP+BC最长
如图3,当BP⊥MN时,BP最短
∵S△NBM=S△ABO,MN=OA=5
∴![]() MNBP=
MNBP=![]() OByA
OByA
∴BP=![]() =
=![]() =
=![]()
∴CP最小值=![]() 3=
3=![]()
当点P与M重合时,BP最大,BP=BM=OB=6
∴CP最大值=6+3=9
∴线段CP长的取值范围为![]() .
.