题目内容
(2009•惠山区二模)二次函数y=ax2+bx+c的图象的一部分如图所示.已知它的顶点M在第二象限,且经过点A(1,0)和点B(0,1).(1)试求a,b所满足的关系式;
(2)设此二次函数的图象与x轴的另一个交点为C,当△AMC的面积为△ABC面积的
 倍时,求a的值;
倍时,求a的值;(3)是否存在实数a,使得△ABC为直角三角形?若存在,请求出a的值;若不存在,请说明理由.

【答案】分析:(1)把点A(1,0)和点B(0,1)的坐标代入抛物线的解析式,就可以得到关于a,b,c关系式.整理就得到a,b的关系.
(2)△ABC的面积可以求出是 ,利用公式求出抛物线的顶点的纵坐标,进而表示出△AMC的面积,根据
,利用公式求出抛物线的顶点的纵坐标,进而表示出△AMC的面积,根据 ,就可以得到关于a的方程,解得a的值.
,就可以得到关于a的方程,解得a的值.
(3)本题应分A是直角顶点,B是直角顶点,C是直角顶点三种情况进行讨论.
解答:解:(1)将A(1,0),B(0,l)代入y=ax2+bx+c,
得: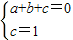 ,
,
可得:a+b=-1(2分)
(2)∵a+b=-1,
∴b=-a-1代入函数的解析式得到:y=ax2-(a+1)x+1,
顶点M的纵坐标为 ,
,
因为 ,
,
由同底可知: ,(3分)
,(3分)
整理得:a2+3a+1=0,
解得: (4分)
(4分)
由图象可知:a<0,
因为抛物线过点(0,1),顶点M在第二象限,其对称轴x= ,
,
∴-1<a<0,
∴ 舍去,
舍去,
从而 .(5分)
.(5分)
(3)①由图可知,A为直角顶点不可能;(6分)
②若C为直角顶点,此时C点与原点O重合,不合题意;(7分)
③若设B为直角顶点,则可知AC2=AB2+BC2,
令y=0,可得:0=ax2-(a+1)x+1,
解得:x1=1,x2=
得:AC=1- ,BC=
,BC= ,AB=
,AB= .
.
则(1- )2=(1+
)2=(1+ )+2,
)+2,
解得:a=-1,由-1<a<0,不合题意.
所以不存在.(9分)
综上所述:不存在.(10分)
点评:本题值函数与三角形相结合的题目,注意数与形的结合是解题的关键.
(2)△ABC的面积可以求出是
 ,利用公式求出抛物线的顶点的纵坐标,进而表示出△AMC的面积,根据
,利用公式求出抛物线的顶点的纵坐标,进而表示出△AMC的面积,根据 ,就可以得到关于a的方程,解得a的值.
,就可以得到关于a的方程,解得a的值.(3)本题应分A是直角顶点,B是直角顶点,C是直角顶点三种情况进行讨论.
解答:解:(1)将A(1,0),B(0,l)代入y=ax2+bx+c,
得:
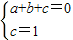 ,
,可得:a+b=-1(2分)
(2)∵a+b=-1,
∴b=-a-1代入函数的解析式得到:y=ax2-(a+1)x+1,
顶点M的纵坐标为
 ,
,因为
 ,
,由同底可知:
 ,(3分)
,(3分)整理得:a2+3a+1=0,
解得:
 (4分)
(4分)由图象可知:a<0,
因为抛物线过点(0,1),顶点M在第二象限,其对称轴x=
 ,
,∴-1<a<0,
∴
 舍去,
舍去,从而
 .(5分)
.(5分)(3)①由图可知,A为直角顶点不可能;(6分)
②若C为直角顶点,此时C点与原点O重合,不合题意;(7分)
③若设B为直角顶点,则可知AC2=AB2+BC2,
令y=0,可得:0=ax2-(a+1)x+1,
解得:x1=1,x2=

得:AC=1-
 ,BC=
,BC= ,AB=
,AB= .
.则(1-
 )2=(1+
)2=(1+ )+2,
)+2,解得:a=-1,由-1<a<0,不合题意.
所以不存在.(9分)
综上所述:不存在.(10分)
点评:本题值函数与三角形相结合的题目,注意数与形的结合是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 倍时,求a的值;
倍时,求a的值;
 倍时,求a的值;
倍时,求a的值;
 倍时,求a的值;
倍时,求a的值;
 倍时,求a的值;
倍时,求a的值;