题目内容
(2004•济南)已知等边△ABC边长为a,D、E分别为AB、AC边上的动点,且在运动时保持DE∥BC,如图(1),⊙O1与⊙O2都不在△ABC的外部,且⊙O1、⊙O2分别与∠B和∠C的两边及DE都相切,其中和DE、BC的切点分别为M、N、M′、N′.(1)求证:⊙O1和⊙O2是等圆;
(2)设⊙O1的半径长为x,圆心距O1O2为y,求y与x的函数关系式,并写出x的取值范围;
(3)当⊙O1与⊙O2外切时,求x的值;
(4)如图(2),当D、E分别是AB、AC边的中点时,将⊙O2先向左平移至和⊙O1重合,然后将重合后的圆沿着△ABC内各边按图(2)中箭头的方向进行滚动,且总是与△ABC的边相切,当点O1第一次回到它原来的位置时,求点O1经过的路线长度?

【答案】分析:(1)根据连接圆的两条平行切线的切点的线段是直径,以及切线的性质判定四边形是矩形,再根据矩形的性质即可证明;
(2)根据30°的直角三角形的性质,分别用圆的半径表示出BM′和CN′的长,即可写出y与x的函数关系式;根据y=0,即可求得x的最大值;
(3)根据两圆外切,圆心距等于两圆半径之和,再结合(2)中的函数关系式求得x的值;
(4)首先根据等边三角形的高,结合三角形的中位线定理求得x的值;
再根据⊙O1的圆心O1所经过的路线,是与△ABC相似,且各边与△ABC各边距离为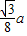 的正三角形.
的正三角形.
结合等边三角形的性质进行计算.
解答:解:(1)连接MM′、NN′.
∵DE和BC是⊙O1的切线,DE∥BC,
∴MM′过点O1.同理NN'过点O2.∵MM′⊥BC,MM′⊥DE,NN′⊥BC
∴四边形MM′N′N是矩形.
∴MM′=NN′,即⊙O1和⊙O2是等圆;
(2)连接OlB,OlO2,O2C,OlM′,O2N′.
易证四边形O1BCO2是等腰梯形,四边形O1M′N′O2是矩形.
在Rt△O1BM′中,∠01BM′=30°,OlM′=x,
则BM′=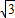 x.
x.
∵y=O12=M′N′,BM′=N′C= x,BC=BM′+M′N′+N′C,
x,BC=BM′+M′N′+N′C,
∴y+2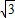 =a,
=a,
∴y=a-2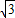 x,
x,
求得0<x≤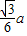 ;
;
(3)当⊙Ol和⊙O2外切时,OlO2=2x,2x=a-2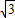 x,
x,
∴x=( -1)
-1)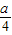 ;
;
(4)当DE是△ABC的中位线时,求得x=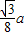 .
.
此时BM'= x=
x= a.
a.
⊙O1的圆心O1所经过的路线是与△ABC相似,且各边与△ABC各边距离为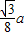 的正三角形.
的正三角形.
其边长为a- a×2=
a×2=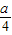 ,
,
∴所求的圆心O1走过的长度为: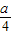 ×3=
×3= a.
a.
点评:综合运用了等边三角形的性质、矩形的判定和性质以及两圆的位置关系和数量之间的联系.
(2)根据30°的直角三角形的性质,分别用圆的半径表示出BM′和CN′的长,即可写出y与x的函数关系式;根据y=0,即可求得x的最大值;
(3)根据两圆外切,圆心距等于两圆半径之和,再结合(2)中的函数关系式求得x的值;
(4)首先根据等边三角形的高,结合三角形的中位线定理求得x的值;
再根据⊙O1的圆心O1所经过的路线,是与△ABC相似,且各边与△ABC各边距离为
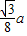 的正三角形.
的正三角形.结合等边三角形的性质进行计算.
解答:解:(1)连接MM′、NN′.
∵DE和BC是⊙O1的切线,DE∥BC,
∴MM′过点O1.同理NN'过点O2.∵MM′⊥BC,MM′⊥DE,NN′⊥BC

∴四边形MM′N′N是矩形.
∴MM′=NN′,即⊙O1和⊙O2是等圆;
(2)连接OlB,OlO2,O2C,OlM′,O2N′.
易证四边形O1BCO2是等腰梯形,四边形O1M′N′O2是矩形.
在Rt△O1BM′中,∠01BM′=30°,OlM′=x,
则BM′=
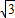 x.
x.∵y=O12=M′N′,BM′=N′C=
 x,BC=BM′+M′N′+N′C,
x,BC=BM′+M′N′+N′C,∴y+2
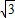 =a,
=a,∴y=a-2
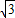 x,
x,求得0<x≤
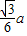 ;
;(3)当⊙Ol和⊙O2外切时,OlO2=2x,2x=a-2
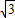 x,
x,∴x=(
 -1)
-1)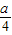 ;
;(4)当DE是△ABC的中位线时,求得x=
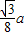 .
.此时BM'=
 x=
x= a.
a.⊙O1的圆心O1所经过的路线是与△ABC相似,且各边与△ABC各边距离为
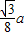 的正三角形.
的正三角形.其边长为a-
 a×2=
a×2=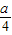 ,
,∴所求的圆心O1走过的长度为:
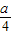 ×3=
×3= a.
a.点评:综合运用了等边三角形的性质、矩形的判定和性质以及两圆的位置关系和数量之间的联系.

练习册系列答案
相关题目
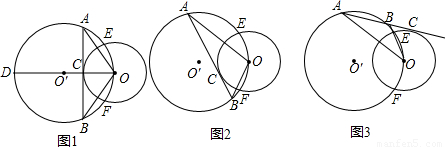
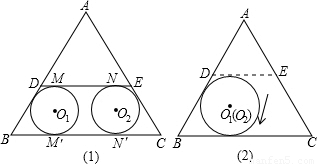
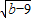 =0,计算
=0,计算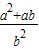 •
•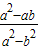 的值.
的值. x2+(6-
x2+(6-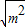 )x+m-3与x轴有A、B两个交点,且A、B两点关于y轴对称.
)x+m-3与x轴有A、B两个交点,且A、B两点关于y轴对称.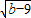 =0,计算
=0,计算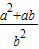 •
• 的值.
的值.