题目内容
【题目】如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,

(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
【答案】(1)证明见解析(2)4
【解析】解:(1)证明:∵∠APC和∠ABC是同弧所对的圆周角,∴∠APC=∠ABC。
又∵在△ABC中,∠BAC=∠APC=60°,∴∠ABC=60°。
∴∠ACB=180°﹣∠BAC﹣∠ABC=180°﹣60°﹣60°=60°。
∴△ABC是等边三角形。
(2)连接OB,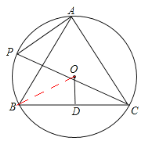
∵△ABC为等边三角形,⊙O为其外接圆,
∴O为△ABC的外心。
∴BO平分∠ABC。∴∠OBD=30°.∴OD=8×![]() =4。
=4。
(1)根据同弧所对的圆周角相等的性质和已知∠BAC=∠APC=60°可得△ABC的每一个内角都等于600,从而得证。
(2)根据等边三角形三线合一的性质,得含30度角直角三角形OBD,从而根据30度角所对边是斜边一半的性质,得OD=8×![]() =4
=4

练习册系列答案
相关题目
【题目】某学习小组做了一个实验:从一幢100 m高的楼顶随手放下一只苹果,测得有关数据如下:
下落时间t(s) | 1 | 2 | 3 | 4 |
下落高度h(m) | 5 | 20 | 45 | 80 |
则下列说法错误的是( )
A. 苹果每秒下落的路程越来越长 B. 苹果每秒下落的路程不变
C. 苹果下落的速度越来越快 D. 可以推测,苹果落到地面的时间不超过5秒
【题目】某公司有10名销售员,去年完成销售额情况如下表:
销售额(元) | 3 | 4 | 5 | 6 | 7 | 8 | 10 |
销售人员(人) | 1 | 3 | 2 | 1 | 1 | 1 | 1 |
已知销售额的平均数为5.6万元,众数为4万元,中位数为5万元.今年公司为了调动员工的积极性,提高年销售额,准备采取超额有奖的措施,根据以上信息,确定万元为销售额标准.
