题目内容
有n个数,从第二个数开始,每一个数都比它前面相邻的数大3,即4,7,…,3n+1,且它们相乘的积的末尾恰有32个0.则n的最小值为 .
【答案】分析:先把(3n+1)÷5化为2+3(n-3)÷5的形式,再根据这n个数中,只有第3,8,13,18,个数是5的倍数,它们每5个中恰有1个是25的倍数,每25个中恰有1个是125的倍,找出规律即可求出n的值.
解答:解:∵(1+3n)÷5=2+3(n-3)÷5,
∴这n个数中,只有第3,8,13,18,个数是5的倍数,它们是5×2,5×5,5×8,5×11,
它们每5个中恰有1个是25的倍数,每25个中恰有1个是125的倍数,
∴(5×2)×(5×5)×(5×8)××(5×77)=532×A,其中,A不是5的倍数,
∴5×77=3n+1,
∴n=128.
故答案为:128.
点评:本题考查的是尾数的特征,根据题意把(1+3n)÷5化为2+3(n-3)÷5的形式是解答此题的关键.
解答:解:∵(1+3n)÷5=2+3(n-3)÷5,
∴这n个数中,只有第3,8,13,18,个数是5的倍数,它们是5×2,5×5,5×8,5×11,
它们每5个中恰有1个是25的倍数,每25个中恰有1个是125的倍数,
∴(5×2)×(5×5)×(5×8)××(5×77)=532×A,其中,A不是5的倍数,
∴5×77=3n+1,
∴n=128.
故答案为:128.
点评:本题考查的是尾数的特征,根据题意把(1+3n)÷5化为2+3(n-3)÷5的形式是解答此题的关键.

练习册系列答案
相关题目
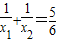 ;
;