题目内容
若圆内接正三角形的边长为2，则圆的半径为分析：画图，利用正三角形的性质找到由内切圆半径，外接圆半径和边长的一半所组成的三角形（如△OBD），然后进行计算可求出外接圆半径．
解答：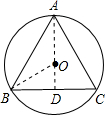
解：如图，△ABC是⊙O的边长为2的内接正三角形．
连OB，OA，
∵△ABC是正三角形，
∴AO垂直平分BC，设垂足为D．
∴BD=1；
又∵∠OBD=30°，
∴OD=
，则OB=
=
，
故填
．
解：如图，△ABC是⊙O的边长为2的内接正三角形．连OB，OA，
∵△ABC是正三角形，
∴AO垂直平分BC，设垂足为D．
∴BD=1；
又∵∠OBD=30°，
∴OD=
| 1 | ||
|
| 2 | ||
|
2
| ||
| 3 |
故填
2
| ||
| 3 |
点评：熟悉正三角形的性质．它的内心，外心等是重合的．记住含30度的直角三角形三边之间的数量关系（1：
：2）以及正三角形的内切圆半径，外接圆半径和它的高的比（1：2：3）．
| 3 |
练习册系列答案
暑假作业海燕出版社系列答案
相关题目