题目内容
直角三角形的两直角边长分别为a,b,且a+b=17,a2+b2=169,则此直角三角形的面积为
30
30
.分析:先根据a+b=17得出(a+b)2=289,再把a2+b2=169代入求出ab的值,进而可得出此直角三角形的面积.
解答:解:∵直角三角形的两直角边长分别为a,b,且a+b=17,
∴(a+b)2=289,即a2+b2+2ab=289,
∵a2+b2=169,
∴2ab=289-169=120,
∴ab=60,
∴此直角三角形的面积=
ab=
×60=30.
故答案为:30.
∴(a+b)2=289,即a2+b2+2ab=289,
∵a2+b2=169,
∴2ab=289-169=120,
∴ab=60,
∴此直角三角形的面积=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:30.
点评:本题考查的是勾股定理,在解答此题时要注意完全平方公式的运用.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
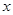 ,
,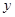 表示直角三角形的两直角边(
表示直角三角形的两直角边(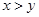 ),下列四个说法:
),下列四个说法:
 ,②
,②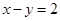 ,③
,③ ,④
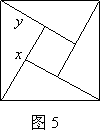
,④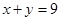 .
.
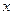 ,
,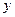 表示直角三角形的两直角边(
表示直角三角形的两直角边(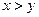 ),下列四个说法:
),下列四个说法: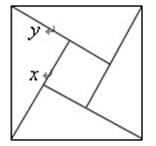
 ,②
,② ,③
,③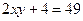 ,④
,④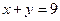 .
.