题目内容
(本小题满分8分)

如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).(参考数据:≈1.73,
sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)

如图,大海中有A和B两个岛屿,为测量它们之间的距离,在海岸线PQ上点E处测得∠AEP=74°,∠BEQ=30°;在点F处测得∠AFP=60°,∠BFQ=60°,EF=1km.
(1)判断AB、AE的数量关系,并说明理由;
(2)求两个岛屿A和B之间的距离(结果精确到0.1km).(参考数据:≈1.73,
sin74°≈0.96,cos74°≈0.28,tan74°≈3.49,sin76°≈0.97,cos76°≈0.24)
 |
(1)相等,证明:∵∠BEQ=30°,∠BFQ=60°,∴∠EBF=30°,∴EF=BF.
又∵∠AFP=60°,∴∠BFA=60°.
在△AEF与△ABF中,EF=BF,∠AFE=∠AFB,AF=AF,
∴△AEF≌△ABF,∴AB=AE. ………………………………………… 4分
(2)作AH⊥PQ,垂足为H,设AE=x,
则AH=xsin74°,HE=xcos74°,HF=xcos74°+1.
Rt△AHF中,AH=HF·tan60°,∴xcos74°=(xcos74°+1)·tan60°,即0.96x=(0.28x+1)×1.73,
∴x≈3.6,即AB≈3.6 km.答:略.…………………………………………8分
此题考查的知识点有三角形全等、三角函数的计算。

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
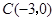 ,点
,点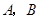 分别在
分别在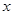 轴,
轴,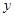 轴的正半轴上,且满足
轴的正半轴上,且满足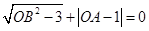 .
.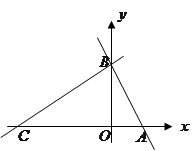
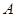 ,点
,点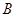 的坐标
的坐标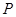 从
从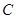 点出发,以每秒1个单位的速度沿线段
点出发,以每秒1个单位的速度沿线段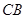 运动,连结
运动,连结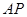 .设
.设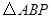 的面积为
的面积为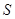 ,点
,点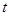 秒,求
秒,求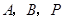 为顶点的三角形与
为顶点的三角形与 相似?若存在,请直接写出点
相似?若存在,请直接写出点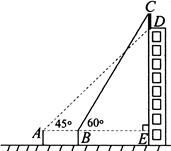

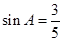 ,那么
,那么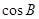 的值等于( )
的值等于( )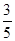 B.
B.  C.
C.  D.
D.