题目内容
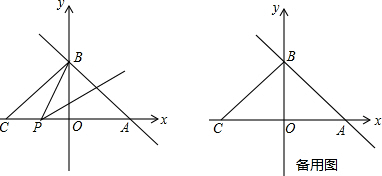
（2012•邵阳）如图所示，在Rt△ABC中，∠ACB=90°，∠B=30°，ED是BC的垂直平分线，请写出图中两条相等的线段是BD=CD（答案不唯一）
BD=CD（答案不唯一）
．分析：由ED是BC的垂直平分线，可得BE=CE，BD=CD，又由在Rt△ABC中，∠ACB=90°，∠B=30°，易证得△AEC是等边三角形，即可得AE=EC=AC=BE．
解答：解：∵ED是BC的垂直平分线，
∴BE=CE，BD=CD，
∵在Rt△ABC中，∠ACB=90°，∠B=30°，
∴∠ECB=∠B=30°，∠A=90°-∠B=60°，
∴∠ACE=90°-30°=60°，
∴△AEC是等边三角形，
∴AE=EC=AC，
∴AE=AC=EC=BE．
∴图中两条相等的线段是：BE=CE=AC=BE或BD=CD．
故答案为：此题答案不唯一，如BD=CD等．
∴BE=CE，BD=CD，
∵在Rt△ABC中，∠ACB=90°，∠B=30°，
∴∠ECB=∠B=30°，∠A=90°-∠B=60°，
∴∠ACE=90°-30°=60°，
∴△AEC是等边三角形，
∴AE=EC=AC，
∴AE=AC=EC=BE．
∴图中两条相等的线段是：BE=CE=AC=BE或BD=CD．
故答案为：此题答案不唯一，如BD=CD等．
点评：此题考查了线段垂直平分线的性质、等边三角形的判定与性质以及含30°角的直角三角形的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
（2012•邵阳）如图所示，圆柱体的俯视图是（ ）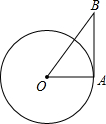
（2012•邵阳）如图所示，直线AB是⊙O的切线，切点为A，OB=5，AB=4，则OA的长是
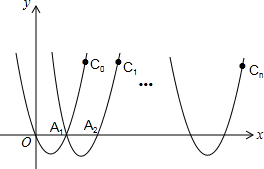（2012•邵阳）如图所示，已知抛物线C0的解析式为y=x2-2x