题目内容
【题目】如图①,正方形A的一个顶点与正方形B的对称中心重合,重叠部分面积是正方形A面积的![]() ,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A的对称中心重合,则重叠部分面积是正方形B面积的( )
,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A的对称中心重合,则重叠部分面积是正方形B面积的( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
设正方形B的面积为S,正方形B对角线的交点为O,标注字母并过点O作边的垂线,根据正方形的性质可得OE=OM,∠EOM=90°,再根据同角的余角相等求出∠EOF=∠MON,然后利用“角边角”证明△OEF和△OMN全等,根据全等三角形的面积相等可得阴影部分的面积等于正方形B的面积的![]() ,再求出正方形B的面积=2正方形A的面积,即可得出答案.
,再求出正方形B的面积=2正方形A的面积,即可得出答案.
解:设正方形B对角线的交点为O,如图1,
设正方过点O作边的垂线,则OE=OM,∠EOM=90°,
∵∠EOF+∠EON=90°,∠MON+∠EON=90°,
∴∠EOF=∠MON,
在△OEF和△OMN中
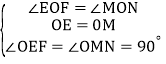 ,
,
∴△OEF≌△OMN(ASA),
∴阴影部分的面积=S四边形NOEP+S△OEF=S四边形NOEP+S△OMN=S四边形MOEP=![]() S正方形CTKW,
S正方形CTKW,
即图1中阴影部分的面积=正方形B的面积的四分之一,
同理图2中阴影部分烦人面积=正方形A的面积的四分之一,
∵图①,正方形A的一个顶点与正方形B的对称中心重合,重叠部分面积是正方形A面积的![]() ,
,
∴正方形B的面积=正方形A的面积的2倍,
∴图2中重叠部分面积是正方形B面积的![]() ,
,
故选:D.


练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目