Question

【题目】聪明好学的亮亮看到一课外书上有个重要补充：

（角平分线定理）三角形一个内角的平分线分对边所成的两条线段与这个角的两邻边对应成比例．于是他就和其他同学研究一番，写出了已知、求证如下：

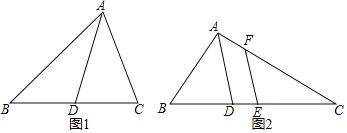
“已知：如图1，△ABC中，AD平分∠BAC交BC于点D，求证：”

可是他们依然找不到证明的方法，于是，老师提示：过点B作BE∥AC交AD延长线于点E，于是得到△BDE∽△CDA，从而打开思路．

（Ⅰ）请你按老师的提示或你认为其他可行的方法帮亮亮完成证明．

（Ⅱ）利用角平分线定理解决如下问题：

如图2，△ABC中，E是BC中点，AD是∠BAC的平分线，EF∥AD交AC于F，AB＝7，AC＝15，求AF的长．

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ）AF＝4

【解析】

（Ⅰ）构造平行线，利用相似三角形的性质解决问题即可．

（Ⅱ）根据角平分线的性质即可得出，结合E是BC中点，即可得出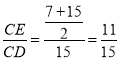，由EF∥AD，得出，进而得出，此题得解．

（Ⅰ）证明：如图1中，过点B作BE∥AC交AD延长线于点E．

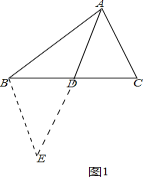
∵BE∥AC，

∴∠E＝∠CAE，

∵∠BAE＝∠CAE，

∴∠BAE＝∠E，

∴BA＝BE，

∵BE∥AC，

∴△BDE∽△CDA，

∴，

∴.

（Ⅱ）解：如图2中，

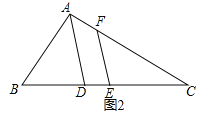
∵AD是∠BAC的平分线，AB＝7，AC＝15，

∴，

∵E是BC中点，

∴，

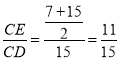∵EF∥AD，

∴，

∴，

∵AC＝15，

∴AF＝4．