题目内容
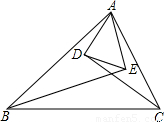
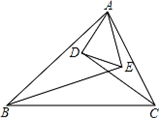
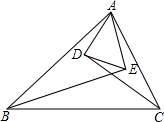 如下图,已知BE、CD分别是△ABC的角平分线,并且AE⊥BE于E点,AD⊥DC于D点.
如下图,已知BE、CD分别是△ABC的角平分线,并且AE⊥BE于E点,AD⊥DC于D点.求证:(1)DE∥BC;(2)DE=
| 1 | 2 |
分析:延长AD、AE分别交BC于F、G;△ABG中,BE是∠ABG的角平分线,且是底边AG的高,易证得△ABG是等腰三角形,则E是AG中点;同理可知D是AF的中点;那么DE即为△AFG的中位线,由此证得DE∥BC,DE=
FG;而FG=BG+CF-BC=AB+AC-BC,由此可证得(2)的结论.
| 1 |
| 2 |
解答: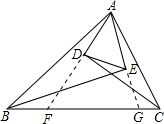 证明:(1)延长AD、AE,交BC于F、G;
证明:(1)延长AD、AE,交BC于F、G;
∵BE⊥AG,
∴∠AEB=∠BEG=90°;
∵BE平分∠ABG,
∴∠ABE=∠GBE;
∴∠BAE=∠BGE;
∴△ABG是等腰三角形;
∴AB=BG,E是AG中点;
同理可得:AC=CF,D是AF中点;
∴DE是△AFG的中位线;
∴DE∥BC.
(2)由(1)知DE是△AFG的中位线,
∴DE=
FG;
∵FG=BG+CF-BC,且AB=BG,AC=CF;
∴FG=AB+AC-BC,即DE=
(AB+AC-BC).
 证明:(1)延长AD、AE,交BC于F、G;
证明:(1)延长AD、AE,交BC于F、G;∵BE⊥AG,
∴∠AEB=∠BEG=90°;
∵BE平分∠ABG,
∴∠ABE=∠GBE;
∴∠BAE=∠BGE;
∴△ABG是等腰三角形;
∴AB=BG,E是AG中点;
同理可得:AC=CF,D是AF中点;
∴DE是△AFG的中位线;
∴DE∥BC.
(2)由(1)知DE是△AFG的中位线,
∴DE=
| 1 |
| 2 |
∵FG=BG+CF-BC,且AB=BG,AC=CF;
∴FG=AB+AC-BC,即DE=
| 1 |
| 2 |
点评:此题主要考查的是等腰三角形的判定和性质以及三角形中位线定理的应用;能够正确的构建出△ABG、△ACF两个等腰三角形是解答此题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 如下图,已知BE、CD分别是△ABC的角平分线,并且AE⊥BE于E点,AD⊥DC于D点.
如下图,已知BE、CD分别是△ABC的角平分线,并且AE⊥BE于E点,AD⊥DC于D点.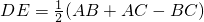 .
. .
.
 .
.
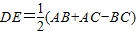 .
.