题目内容
(以下两小题选做一题,第1小题满分14分,第2小题满分为10分.若两小题都做,以第1小题计分)选做第
(1)一张矩形纸片OABC平放在平面直角坐标系内,O为原点,点A在x的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
①如图,将纸片沿CE对折,点B落在x轴上的点D处,求点D的坐标;
②在①中,设BD与CE的交点为P,若点P,B在抛物线y=x2+bx+c上,求b,c的值;
③若将纸片沿直线l对折,点B落在坐标轴上的点F处,l与BF的交点为Q,若点Q在②的抛物线上,求l的解析式.
(2)一张矩形纸片OABC平放在平面直角坐标系内,O为原点,点A在x的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
①求直线AC的解析式;
②若M为AC与BO的交点,点M在抛物线y=-
| 8 | 5 |
③将纸片沿CE对折,点B落在x轴上的点D处,试判断点D是否在②的抛物线上,并说明理由.
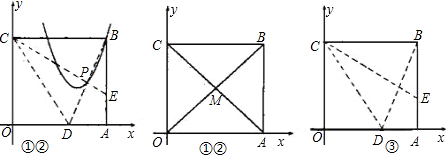
分析:(1)①求D点坐标,关键是求OD的长,根据折叠的性质可知:CD=BC=OA,在直角三角形OCD中,根据OC、CD的长,即可用勾股定理求出OD的值.也就求出了D点的坐标.
②还是根据折叠的性质求解,根据折叠的性质不难得出CE垂直平分BD,即P为BD中点,因此P点横坐标为OD的长加上AD的一半,而P点纵坐标为B点纵坐标的一半,据此可求出P点坐标.然后将P、B的坐标代入抛物线的解析式中即可求出待定系数的值.
③由于F点的位置不确定,可分两种情况:
①当F在x轴上时,Q点纵坐标为B点总坐标的一半,由此可求出Q点纵坐标,将其代入抛物线的解析式中,可求得Q点的坐标.然后根据Q点坐标,然后根据Q点坐标去求直线l与坐标轴其他交点的坐标.
②当F在y轴上时,Q点横坐标为B点横坐标的一半,可将其代入抛物线的解析式中求出Q点坐标,后同①.(本题也可先求出直线BQ的解析式,由于直线l垂直BQ,那么直线l的斜率和直线BQ的斜率的积为-1,又知直线l过Q点可求出直线l的解析式.)
(2)题较简单,参照(1)题部分解题过程即可.
①已知OA=5,OC=4故A(5,0),C(0,4)求出直线AC的解析式为y=-
x+4.
②可知M点坐标为(
,2),设-
(
)2+k•
=2可求得k值.
③已知CD=BC=OA=5,OC=4,∠COD=90°推出D(3,0).当x=3时,y=-
×32+
×3=0,得出点D在抛物线上.
②还是根据折叠的性质求解,根据折叠的性质不难得出CE垂直平分BD,即P为BD中点,因此P点横坐标为OD的长加上AD的一半,而P点纵坐标为B点纵坐标的一半,据此可求出P点坐标.然后将P、B的坐标代入抛物线的解析式中即可求出待定系数的值.
③由于F点的位置不确定,可分两种情况:
①当F在x轴上时,Q点纵坐标为B点总坐标的一半,由此可求出Q点纵坐标,将其代入抛物线的解析式中,可求得Q点的坐标.然后根据Q点坐标,然后根据Q点坐标去求直线l与坐标轴其他交点的坐标.
②当F在y轴上时,Q点横坐标为B点横坐标的一半,可将其代入抛物线的解析式中求出Q点坐标,后同①.(本题也可先求出直线BQ的解析式,由于直线l垂直BQ,那么直线l的斜率和直线BQ的斜率的积为-1,又知直线l过Q点可求出直线l的解析式.)
(2)题较简单,参照(1)题部分解题过程即可.
①已知OA=5,OC=4故A(5,0),C(0,4)求出直线AC的解析式为y=-
| 4 |
| 5 |
②可知M点坐标为(
| 5 |
| 2 |
| 8 |
| 5 |
| 5 |
| 2 |
| 5 |
| 2 |
③已知CD=BC=OA=5,OC=4,∠COD=90°推出D(3,0).当x=3时,y=-
| 8 |
| 5 |
| 24 |
| 5 |
解答:解:(1)①根据题意知,CD=CB=OA=5
∵∠COD=90°
∴CD=
=3
∴D点坐标为(3,0)
②过P作PG⊥x轴于G
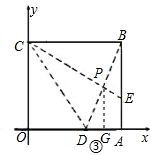
据题知,PG=
AB=2,DG=
AD=1
∴P点坐标(4,2)
∵点P,B在抛物线y=x2+bx+c上
∴b=-7,c=14
③当点F在x轴上时,过Q作QM⊥x轴于M
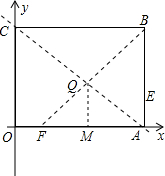
同②可知QM=
AB=2,则Q点的纵坐标为2
得x2-7x+14=2
∴x=3或x=4
∴Q点的坐标为(3,2)或(4,2)
当Q点坐标为(3,2)时,如图,OM=3,MA=2,FA=4
AB=4
FA=AB,而l为BF的中垂线
∴点A在l上
∴l的解析式为y=-x+5.
当Q点坐标为(4,2)时,如图,OM=4,MA=1,OF=3,CF=5,而CB=5;
∴CF=CB
∵l为BF的中垂线
∴点C在l上.
∴l的解析式为y=-
x+4.
当点F在y轴上时,可求得Q(
,
),l与y轴的交点为(0,
)
∴l的解析式为y=-2x+
综上所述,l的解析式为y=-x+5或y=-
x+4或y=-2x+
.
(2)①∵OA=5,OC=4,
∴A(5,0),C(0,4);
∴直线AC的解析式为y=-
x+4.
②可知:M点坐标为(
,2).
由题设知:-
(
)2+k•
=2.
∴k=
③∵CD=BC=OA=5,OC=4,∠COD=90°
∴OD=3,即D(3,0).
当x=3时,y=-
×32+
×3=0
∴点D在抛物线上.
∵∠COD=90°
∴CD=
| CD2-OC2 |
∴D点坐标为(3,0)
②过P作PG⊥x轴于G

据题知,PG=
| 1 |
| 2 |
| 1 |
| 2 |
∴P点坐标(4,2)
∵点P,B在抛物线y=x2+bx+c上
∴b=-7,c=14
③当点F在x轴上时,过Q作QM⊥x轴于M

同②可知QM=
| 1 |
| 2 |
得x2-7x+14=2
∴x=3或x=4
∴Q点的坐标为(3,2)或(4,2)
当Q点坐标为(3,2)时,如图,OM=3,MA=2,FA=4
AB=4
FA=AB,而l为BF的中垂线
∴点A在l上
∴l的解析式为y=-x+5.
当Q点坐标为(4,2)时,如图,OM=4,MA=1,OF=3,CF=5,而CB=5;
∴CF=CB
∵l为BF的中垂线
∴点C在l上.
∴l的解析式为y=-
| 1 |
| 2 |
当点F在y轴上时,可求得Q(
| 5 |
| 2 |
| 11 |
| 4 |
| 31 |
| 4 |
∴l的解析式为y=-2x+
| 31 |
| 4 |
综上所述,l的解析式为y=-x+5或y=-
| 1 |
| 2 |
| 31 |
| 4 |
(2)①∵OA=5,OC=4,
∴A(5,0),C(0,4);
∴直线AC的解析式为y=-
| 4 |
| 5 |
②可知:M点坐标为(
| 5 |
| 2 |
由题设知:-
| 8 |
| 5 |
| 5 |
| 2 |
| 5 |
| 2 |
∴k=
| 24 |
| 5 |
③∵CD=BC=OA=5,OC=4,∠COD=90°
∴OD=3,即D(3,0).
当x=3时,y=-
| 8 |
| 5 |
| 24 |
| 5 |
∴点D在抛物线上.
点评:本题考查了矩形的性质、二次函数解析式的确定、图形的翻折变换等知识,(1)③中要注意F点的位置是坐标轴而不是x轴,因此要分类讨论,不要漏解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 x2+kx上,求k的值;
x2+kx上,求k的值;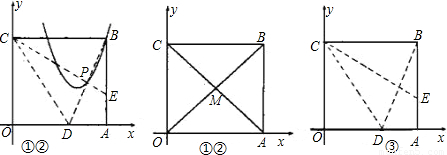
 x2+kx上,求k的值;
x2+kx上,求k的值;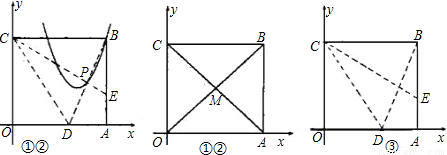
 x2+kx上,求k的值;
x2+kx上,求k的值;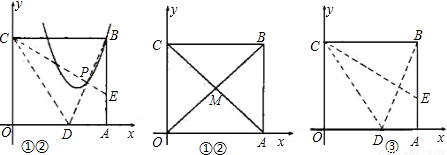
 x2+kx上,求k的值;
x2+kx上,求k的值;