题目内容
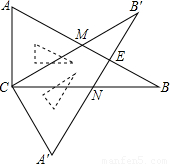
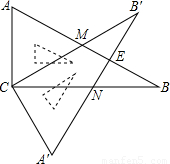
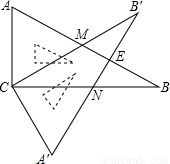
(2008•达州)含30°角的直角三角板ABC(∠B=30°)绕直角顶点C沿逆时针方向旋转角α(∠α<90°),再沿∠A的对边翻折得到△A′B′C,AB与B′C交于点M,A′B′与BC交于点N,A′B′与AB相交于点E.(1)求证:△ACM≌△A′CN;
(2)当∠α=30°时,找出ME与MB′的数量关系,并加以说明.
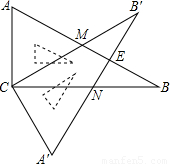
【答案】分析:(1)要证△ACM≌△A'CN,根据已知,只需证∠ACM=∠A′CN.
很明显都用90°减去∠BCB′就可以得到.再加上∠A=∠A′,AC=A′C,即可证三角形全等.
(2)根据题意可知,∠MCN=∠α=30°,则∠AMC=∠MCN+∠B=60°,那么∠EMB′=60°.
而∠B′=30°,显然在Rt△MB′E中,ME= MB′.
MB′.
解答:(1)证明:∵∠A=∠A′,AC=A′C,∠ACM=∠A'CN=90°-∠MCN,
∴△ACM≌△A'CN.
(2)解:在Rt△ABC中
∵∠B=30°,∴∠A=90°-30°=60°.
又∵∠α=30°,∴∠MCN=30°,
∴∠ACM=90°-∠MCN=60°.
∴∠EMB′=∠AMC=∠A=∠MCA=60°.
∵∠B′=∠B=30°,
所以三角形MEB′是Rt△MEB′,且∠B′=30°.
所以MB′=2ME.
点评:本题利用了全等三角形的判定和性质,旋转和对折后得到的图形和原来的图形全等的知识.
很明显都用90°减去∠BCB′就可以得到.再加上∠A=∠A′,AC=A′C,即可证三角形全等.
(2)根据题意可知,∠MCN=∠α=30°,则∠AMC=∠MCN+∠B=60°,那么∠EMB′=60°.
而∠B′=30°,显然在Rt△MB′E中,ME=
 MB′.
MB′.解答:(1)证明:∵∠A=∠A′,AC=A′C,∠ACM=∠A'CN=90°-∠MCN,
∴△ACM≌△A'CN.
(2)解:在Rt△ABC中
∵∠B=30°,∴∠A=90°-30°=60°.
又∵∠α=30°,∴∠MCN=30°,
∴∠ACM=90°-∠MCN=60°.
∴∠EMB′=∠AMC=∠A=∠MCA=60°.
∵∠B′=∠B=30°,
所以三角形MEB′是Rt△MEB′,且∠B′=30°.
所以MB′=2ME.
点评:本题利用了全等三角形的判定和性质,旋转和对折后得到的图形和原来的图形全等的知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
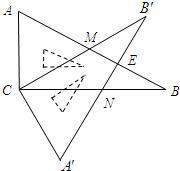 (2008•达州)含30°角的直角三角板ABC(∠B=30°)绕直角顶点C沿逆时针方向旋转角α(∠α<90°),再沿∠A的对边翻折得到△A′B′C,AB与B′C交于点M,A′B′与BC交于点N,A′B′与AB相交于点E.
(2008•达州)含30°角的直角三角板ABC(∠B=30°)绕直角顶点C沿逆时针方向旋转角α(∠α<90°),再沿∠A的对边翻折得到△A′B′C,AB与B′C交于点M,A′B′与BC交于点N,A′B′与AB相交于点E.