题目内容
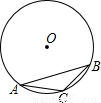
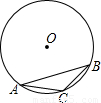
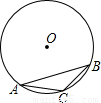
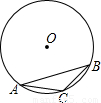
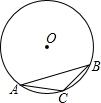 如图,在⊙O内,AB是内接正六边形的一边,AC是内接正十边形的一边,BC是内接正n边形的一边,那么n=________.
如图,在⊙O内,AB是内接正六边形的一边,AC是内接正十边形的一边,BC是内接正n边形的一边,那么n=________.
15
分析:根据AB是内接正六边形的一边,AC是内接正十边形的一边,求出∠AOB、∠AOC、∠BOC的度数,进而可得∠BOC的度数,判断出n的值.
解答: 解:连接OA、OC、OB.
解:连接OA、OC、OB.
因为AB是内接正六边形的一边,
所以∠AOB=360°× =60°;
=60°;
因为AC是内接正十边形的一边,
所以∠AOC=360°× =36°.
=36°.
则∠BOC=60°-36°=24°,
又因为360°÷24=15,
所以n=15.
故答案为:15.
点评:此题主要考查正多边形的计算问题,属于常规题.
分析:根据AB是内接正六边形的一边,AC是内接正十边形的一边,求出∠AOB、∠AOC、∠BOC的度数,进而可得∠BOC的度数,判断出n的值.
解答:
 解:连接OA、OC、OB.
解:连接OA、OC、OB.因为AB是内接正六边形的一边,
所以∠AOB=360°×
 =60°;
=60°;因为AC是内接正十边形的一边,
所以∠AOC=360°×
 =36°.
=36°.则∠BOC=60°-36°=24°,
又因为360°÷24=15,
所以n=15.
故答案为:15.
点评:此题主要考查正多边形的计算问题,属于常规题.

练习册系列答案
相关题目
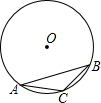 如图,在⊙O内,AB是内接正六边形的一边,AC是内接正十边形的一边,BC是内接正n边形的一边,那么n=
如图,在⊙O内,AB是内接正六边形的一边,AC是内接正十边形的一边,BC是内接正n边形的一边,那么n=