题目内容

△ABC中，若|cotA-1|+(cosB-
2
2
)2=0，则△ABC为（　　）
A、等腰三角形
B、直角三角形
C、等腰三角形或直角三角形
D、等腰直角三角形
分析：根据非负数的性质求出cotA=1，cosB=
2
2
求出∠A、∠B的值，再根据三角形内角和定理解答即可．
解答：解：∵|cotA-1|+(cosB-
2
2
)2=0，
∴cotA=1，cosB=
2
2
，
∴∠A=∠B=45°，
∴∠C=90°．
∴△ABC为等腰直角三角形．
故选D．
点评：本题考查了特殊角的三角函数值和等腰直角三角形的判定．
练习册系列答案
相关题目
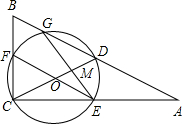精英家教网如图，在△ABC中∠ACB=90°，D是AB的中点，以DC为直径的⊙O交△ABC的三边，交点分别是G，F，E点．GE，CD的交点为M，且ME=4
6
，MD：CO=2：5．
（1）求证：∠GEF=∠A；
（2）求⊙O的直径CD的长；
（3）若cos∠B=0.6，以C为坐标原点，CA，CB所在的直线分别为X轴和Y轴，建立平面直角坐标系，求直线AB的函数表达式．
21、如图①，△ABC中，AB=AC，∠B、∠C的平分线交于O点，过O点作EF∥BC交AB、AC于E、F．试回答：
（1）图中等腰三角形是
△AEF、△OEB、△OFC、△OBC、△ABC
．猜想：EF与BE、CF之间的关系是
EF=BE+CF
．理由：
（2）如图②，若AB≠AC，图中等腰三角形是
△EOB、△FOC
．在第（1）问中EF与BE、CF间的关系还存在吗？
（3）如图③，若△ABC中∠B的平分线BO与三角形外角平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F．这时图中还有等腰三角形吗？EF与BE、CF关系又如何？说明你的理由
28、已知如图1：△ABC中，AB=AC，∠B、∠C的平分线相交于点O，过点O作EF∥BC交AB、AC于E、F．
①图中有几个等腰三角形？请说明EF与BE、CF间有怎样的关系．

②若AB≠AC，其他条件不变，如图2，图中还有等腰三角形吗？如果有，请分别指出它们．另第①问中EF与BE、CF间的关系还存在吗？
③若△ABC中，∠B的平分线与三角形外角∠ACD的平分线CO交于O，过O点作OE∥BC交AB于E，交AC于F．如图3，这时图中还有哪几个等腰三角形？EF与BE、CF间的关系如何？为什么？
认真阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题．

探究1：如图1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，分析发现∠BOC=90°+
1
2
∠A，理由如下：
∵BO和CO分别是∠ABC，∠ACB的角平分线
∴∠1+∠2=
1
2
（∠ABC+∠ACB）=
1
2
（180°-∠A）=90°-
1
2
∠A
∴∠BOC=180°-（∠1+∠2）=180°-（90°-
1
2
∠A）=90°+
1
2
∠A
（1）探究2：如图2中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由．
（2）探究3：如图3中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（直接写出结论）
（3）拓展：如图4，在四边形ABCD中，O是∠ABC与∠DCB的平分线BO和CO的交点，则∠BOC与∠A+∠D有怎样的关系？（直接写出结论）
（4）运用：如图5，五边形ABCDE中，∠BCD、∠EDC的外角分别是∠FCD、∠GDC，CP、DP分别平分∠FCD和∠GDC且相交于点P，若∠A=140°，∠B=120°，∠E=90°，则∠CPD=
95
95
度．
在△ABC 中，若∠A=70°，BO ，CO 分别是∠B ，∠C 的平分线，它们相交于点O ，则∠BOC 的度数为
[     ]
A. 125°    
B. 115°    
C. 110°  
D. 100°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网