题目内容
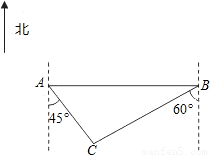
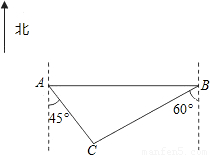
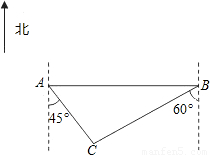
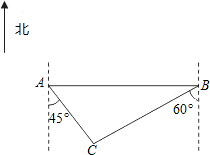
一位祖籍扬州的台商,应市政府的邀请,回乡考察投资环境,谁知家乡的变化竟让他迷路了.他驱车在一条东西走向的公路上由西向东缓慢地前行着.车载GPS(全球卫星定位系统)显示(如图),市政府所在地(点C)在其(点A)南偏东45°的方向上,相距4km.他继续向东前进到达点B的位置,发现市政府所在地在其南偏西60°的方向上.(1)试求该台商由西向东行进的路程AB是多少千米(结果保留根号);
(2)在台商行驶的公路南侧有两条与之平行,且距离这条公路分别约是0.5km的向阳大道和3km的兴宝大道,请估算市政府所在地靠近哪条大道?
【答案】分析:(1)过点C作CD⊥AB于D,利用已知条件分别求得AD、BD的长,那么AB的长就得到了.
(2)让0.5与3分别与CD作差,哪个绝对值小就越靠近其对应的大道.
解答: 解:(1)如图,由题意,可知AC=4,∠DAC=45°,∠ABC=30°,
解:(1)如图,由题意,可知AC=4,∠DAC=45°,∠ABC=30°,
过点C作CD⊥AB于D,
在Rt△ACD中,∵AC=4,∠DAC=45°,
∴AD=AC•cos∠DAC=4×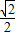 =
=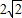 ,CD=AD=
,CD=AD= ,
,
在Rt△BCD中,∵CD=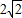 ,∠ABC=30°
,∠ABC=30°
∴BD=CD•cot∠ABC=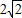 ×
×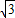 =2
=2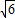 ,
,
∴AB=AD+BD=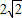 +2
+2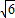
∴该台商由西向东前进了(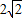 +2
+2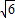 )千米;
)千米;
(2)∵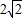 -0.5>3-
-0.5>3-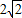
∴市政府所在地靠近兴宝大道.
点评:本题以投资商迷路为背景,考查学生对应用问题的数学化、数学建模思想的掌握情况.解题的关键是将实际问题转化成解直角三角形问题,同时本题还考查了学生估算的技能.
(2)让0.5与3分别与CD作差,哪个绝对值小就越靠近其对应的大道.
解答:
 解:(1)如图,由题意,可知AC=4,∠DAC=45°,∠ABC=30°,
解:(1)如图,由题意,可知AC=4,∠DAC=45°,∠ABC=30°,过点C作CD⊥AB于D,
在Rt△ACD中,∵AC=4,∠DAC=45°,
∴AD=AC•cos∠DAC=4×
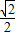 =
=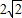 ,CD=AD=
,CD=AD= ,
,在Rt△BCD中,∵CD=
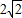 ,∠ABC=30°
,∠ABC=30°∴BD=CD•cot∠ABC=
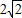 ×
×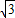 =2
=2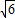 ,
,∴AB=AD+BD=
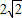 +2
+2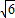
∴该台商由西向东前进了(
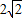 +2
+2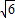 )千米;
)千米;(2)∵
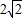 -0.5>3-
-0.5>3-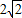
∴市政府所在地靠近兴宝大道.
点评:本题以投资商迷路为背景,考查学生对应用问题的数学化、数学建模思想的掌握情况.解题的关键是将实际问题转化成解直角三角形问题,同时本题还考查了学生估算的技能.

练习册系列答案
相关题目
 阳大道和3km的兴宝大道,请估算市政府所在地靠近哪条大道?
阳大道和3km的兴宝大道,请估算市政府所在地靠近哪条大道?