题目内容
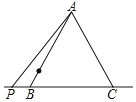
【题目】△ABC是边长为2的等边三角形,点P为直线BC上的动点,把线段AP绕A点逆时针旋转60°至AE,O为AB边上一动点,则OE的最小值为____.
【答案】![]() .
.
【解析】
根据题意连接EC,作CH⊥AB于H,首先证明CE∥AB,再求出平行线之间的距离即可解决问题.
解:如图,连接EC,作CH⊥AB于H.
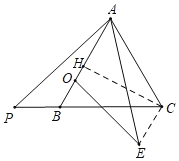
∵△ABC是等边三角形,
∴∠BAC=∠ABC=∠ACB=60°,AB=AC,
∵∠PAE=∠BAC=60°,
∴∠PAB=∠EAC,
∵PA=EQ,BA=CA,
∴△PAB≌△EAC(SAS),
∴∠ABP=∠ACE,
∵∠ABP=180°﹣60°=120°,
∴∠ACE=120°,
∴∠BCE=120°﹣60°=60°,
∴∠ABC=∠BCE,
∴CE∥AB,
∴点E的运动轨迹是直线CE(CE∥AB),
∵CB=CA=AB=2,CH⊥AB,
∴BH=AH=1,
∴CH![]() ,
,
根据垂线段最短,可知OE的最小值=CH![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目