题目内容
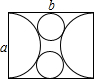 如图,用邻边长为a,b(a<b)的矩形硬纸板截出以a为直径的两个半圆,再截出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b关系式是
如图,用邻边长为a,b(a<b)的矩形硬纸板截出以a为直径的两个半圆,再截出与矩形的较长边、两个半圆均相切的两个小圆,把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,从而做成两个圣诞帽(拼接处材料忽略不计),则a与b关系式是考点:圆锥的计算,相切两圆的性质
专题:
分析:首先利用圆锥形圣诞帽的底面周长等于侧面的弧长求得小圆的半径,然后利用两圆外切的性质求得a、b之间的关系即可.
解答: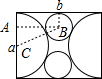 解:∵半圆的直径为a,
解:∵半圆的直径为a,
∴半圆的弧长为
,
∵把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,
∴设小圆的半径为r,则:2πr=
,
解得:r=
,
∴AC=
a-r=
,
如图小圆的圆心为B,半圆的圆心为C,作BA⊥CA于A点,
则:AC2+AB2=BC2
即:(
)2+(
)2=(
+
)2
整理得:b=
a
故答案为:b=
a.
 解:∵半圆的直径为a,
解:∵半圆的直径为a,∴半圆的弧长为
| πa |
| 2 |
∵把半圆作为圆锥形圣诞帽的侧面,小圆恰好能作为底面,
∴设小圆的半径为r,则:2πr=
| πa |
| 2 |
解得:r=
| a |
| 4 |
∴AC=
| 1 |
| 2 |
| a |
| 4 |
如图小圆的圆心为B,半圆的圆心为C,作BA⊥CA于A点,
则:AC2+AB2=BC2
即:(
| a |
| 4 |
| b |
| 2 |
| a |
| 2 |
| a |
| 4 |
整理得:b=
| 2 |
故答案为:b=
| 2 |
点评:本题考查了圆锥的计算,解题的关键是利用两圆相外切的性质得到两圆的圆心距,从而利用勾股定理得到a、b之间的关系.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案
相关题目
下列计算正确的是( )
| A、x2+x4=x6 |
| B、x•x3=x3 |
| C、x6÷x3=x2 |
| D、(-x2y)3=x6y3 |
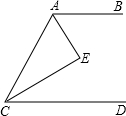 如图,AE、CE平分∠BAC、∠ACD,且∠E=90°,那么AB∥CD,这个结论对吗?为什么?
如图,AE、CE平分∠BAC、∠ACD,且∠E=90°,那么AB∥CD,这个结论对吗?为什么?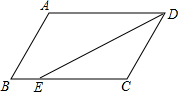 已知如图:?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于E,则BE=
已知如图:?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于E,则BE=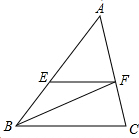 如图,在△ABC中,E、F分别是AB、AC上两点,EF∥BC,BF平分∠ABC,若∠BFE=35°,则∠AEF的度数为
如图,在△ABC中,E、F分别是AB、AC上两点,EF∥BC,BF平分∠ABC,若∠BFE=35°,则∠AEF的度数为