题目内容
 如图,一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD对吗?为什么?
如图,一个弯形管道ABCD的拐角∠ABC=120°,∠BCD=60°,这时说管道AB∥CD对吗?为什么?分析:由已知∠ABC=120°,∠BCD=60°,即∠ABC+∠BCD=120°+60°=180°,可得关于AB∥CD的判定条件:同旁内角互补,两直线平行.
解答:解:说管道AB∥CD是对的.
理由:∵∠ABC=120°,∠BCD=60°
∴∠ABC+∠BCD=180°
∴AB∥CD(同旁内角互补,两直线平行).
理由:∵∠ABC=120°,∠BCD=60°
∴∠ABC+∠BCD=180°
∴AB∥CD(同旁内角互补,两直线平行).
点评:本题考查的是平行线的判定,解答本题的关键是掌握平行线的判定定理:同旁内角互补,两直线平行.

练习册系列答案
相关题目
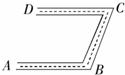 7、如图,一个弯形管道ABCD的拐角∠ABC=110°,要使管道AB,CD保持平行,则∠BCD的度数为( )
7、如图,一个弯形管道ABCD的拐角∠ABC=110°,要使管道AB,CD保持平行,则∠BCD的度数为( ) 12、如图,一个弯形管道ABCD的拐角∠ABC=110°,要使AB∥CD,那么另一个拐角∠BCD应弯成
12、如图,一个弯形管道ABCD的拐角∠ABC=110°,要使AB∥CD,那么另一个拐角∠BCD应弯成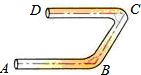 如图,一个弯形管道ABCD的拐角∠ABC=130°.当∠BCD=
如图,一个弯形管道ABCD的拐角∠ABC=130°.当∠BCD=