题目内容
已知:如图,在直角梯形ABCD中,AD∥BC,∠ABC= 90°,DE⊥AC于点F,交BC于点G,交AB的延长线于点 E,且AE=AC。

(1)求证:BG=FG;
(2)若AD=DC=2,求AB的长。
(2)若AD=DC=2,求AB的长。
解:(1)证明:在△ABC和△AFE中,
∵ ,
,
∴△ABC≌△AFE,
∴在△EBG和△CFG中,
∵ ,
,
∴△EBG≌△CFG,
∴BG=FG;
(2)∵AD=DC=2,DE⊥AC,AE=AC,
∴AE=2AF=2AB,
∵∠AFE=∠EAD=90°,
∴△EAF∽△EDA,
∴DE=2AD=4,
∴AE=2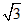 ,
,
∴ 。
。
∵
 ,
,∴△ABC≌△AFE,
∴在△EBG和△CFG中,
∵
 ,
,∴△EBG≌△CFG,
∴BG=FG;
(2)∵AD=DC=2,DE⊥AC,AE=AC,
∴AE=2AF=2AB,
∵∠AFE=∠EAD=90°,
∴△EAF∽△EDA,
∴DE=2AD=4,
∴AE=2
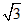 ,
,∴
 。
。
练习册系列答案
相关题目

