题目内容
已知⊙O半径为1cm,P为⊙O外一点,PA切⊙O于点A,PA=1cm,AB是⊙O的弦,且AB=| 2 |
分析:先利用勾股定理逆定理求出∠AOB是直角,再利用一组对边平行且相等得到四边形APBO是平行四边形,从而PB的长等于半径OA.另当B在右侧时,还需讨论.
解答: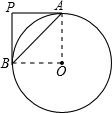 解:连接OA、OB.
解:连接OA、OB.
∵OA=OB=1,AB=
,
∴根据勾股定理的逆定理,得∠AOB=90°,
根据切线的性质定理,得∠OAP=90°,则AP∥OB,
又AP=OB=1,所以四边形PAOB是平行四边形,
所以PB=OA=1.
当B在右侧时,PB=
.
 解:连接OA、OB.
解:连接OA、OB.∵OA=OB=1,AB=
| 2 |
∴根据勾股定理的逆定理,得∠AOB=90°,
根据切线的性质定理,得∠OAP=90°,则AP∥OB,
又AP=OB=1,所以四边形PAOB是平行四边形,
所以PB=OA=1.
当B在右侧时,PB=
| 5 |
点评:能够根据勾股定理的逆定理发现直角三角形,进一步发现特殊四边形平行四边形.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
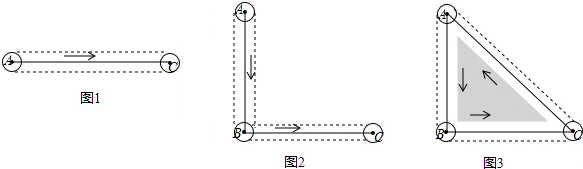

 C方向运动到点C,求圆扫过的区域面积;
C方向运动到点C,求圆扫过的区域面积;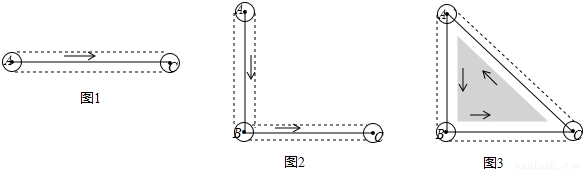
 C方向运动到点C,求圆扫过的区域面积;
C方向运动到点C,求圆扫过的区域面积;