题目内容
如图，两个班的学生分别在M、N两处参加植树劳动，现要在道路AB、AC的交叉区域内设一个茶水供应点P，使P到两条道路的距离相等，且使PM=PN，有一同学说：“只要作一个角平分线、一条线段的垂直平分线，这个茶水供应点的位置就确定了”，你认为这位同学说得对吗？请说明理由，并通过作图找出这一点，不写作法，保留作图痕迹．分析：根据题意可知，∠BAC的角平分线和线段NM的垂直平分线的交点即为P点．
解答：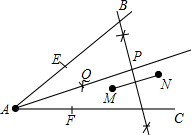
解：A点为圆心，以任意长为半径画弧，交AB与AC于点E、F，
再分别以E、F为圆心，大于
EF长为半径画弧，交于点Q，连接AQ．
即AQ为∠BAC的角平分线．
连接MN，作MN的垂直平分线交AQ于P点．
P点即为所求．
解：A点为圆心，以任意长为半径画弧，交AB与AC于点E、F，再分别以E、F为圆心，大于
| 1 |
| 2 |
即AQ为∠BAC的角平分线．
连接MN，作MN的垂直平分线交AQ于P点．
P点即为所求．
点评：考查了学生在基本作图中角平分线的作法和线段垂直平分线的作法．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
相关题目
20、如图，两个班的学生分别在M、N两处参加植树劳动，现要在道路AB、AC的交叉区域内设一个冷饮供应点P，使P到两条道路的距离相等，且到M、N两劳动处的距离也相等．请在图中找到这个点的位置．（保留作图痕迹，不写作法）
如图，两个班的学生分别在M、N两处参加植树劳动，现要在道路AB、AC的交叉区域内设一个茶水供应点P，使P到两条道路的距离相等，且使P到M、N两地的距离相等．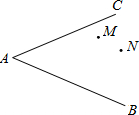
如图，两个班的学生分别在M、N两处参加植树劳动，现要在道路AB、AC的交叉区域内设一茶水供应点P．为节省劳力，要求P到两道路的距离相等，且P到M、N的距离的和最小，问点P应设在何处（保留作图痕迹）．
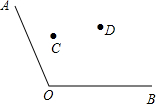如图，两个班的学生分别在C，D两处参加植树劳动，现要在道路AO，OB的交叉区域内设一个茶水供应点M，M到两条道路的距离相等，且MC=MD，这个茶水供应点的位置应建在何处？