题目内容
重庆市垫江县具有2000多年的牡丹种植历史.每年3月下旬至4月上旬,主要分布在该县太平镇、澄溪镇明月山一带的牡丹迎春怒放,美不胜收.由于牡丹之根---丹皮是重要中药材,目前已种植有60多个品种2万余亩牡丹的垫江,因此成为我国丹皮出口基地,获得“丹皮之乡”的美誉.为了提高农户收入,该县决定在现有基础上开荒种植牡丹并实行政府补贴,规定每新种植一亩牡丹一次性补贴农户若干元,经调查,种植亩数y(亩)与补贴数额x(元)之间成一次函数关系,且补贴与种植情况如下表:| 补贴数额(元) | 10 | 20 | … |
| 种植亩数(亩) | 160 | 240 | … |
(1)分别求出政府补贴政策实施后,种植亩数y(亩)、每亩牡丹的收益z(元)与政府补贴数额x(元)之间的函数关系式;
(2)要使全县新种植的牡丹总收益W(元)最大,又要从政府的角度出发,政府应将每亩补贴数额x定为多少元?并求出总收益W的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,为了发展旅游业,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”.已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍.这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元.求混种牡丹的土地有多少亩?(结果精确到个位)(参考数据:
| 2 |
| 3 |
| 5 |
| x |
| 10 |
(2)根据题目条件知道W=y•z,然后分别把(1)中的函数关系式代入其中即可得到W关于x的二次函数,然后利用二次函数的性质即可解决问题;
(3)此时平均每亩收益
| 6120000 |
| 4000 |
依题意得函数图象过(10,160)(20,240),
∴
|
|
∴y=8x+80,
依题意得
z=3000-
| x |
| 10 |
(2)W=y•z=(8x+80)(-3x+3000)
=-24x2+23760x+240000
=-24(x2-990x+4952-4952)+240000
=-24(x-495)2+6120600
∵x为10的整数倍
∴当x=490或x=500时,W最大=6120000
∵从政府角度出发
∴当x=490时,W最大=6120000,
此时种植y=8×490+80=4000亩;
(3)此时平均每亩收益
| 6120000 |
| 4000 |
设混种牡丹的土地m亩,则
(1530+2000)•m-530m-25m2=85000
m2-120m+3400=0
解得:m=60±10
| 2 |
∴m1=60+10
| 2 |
m2=60-10
| 2 |
∴混种牡丹的土地有46亩.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案重庆市垫江县具有2000多年的牡丹种植历史.每年3月下旬至4月上旬,主要分布在该县太平镇、澄溪镇明月山一带的牡丹迎春怒放,美不胜收.由于牡丹之根———丹皮是重要中药材,目前已种植有60多个品种2万余亩牡丹的垫江,因此成为我国丹皮出口基地,获得“丹皮之乡”的美誉。为了提高农户收入,该县决定在现有基础上开荒种植牡丹并实行政府补贴,规定每新种植一亩牡丹一次性补贴农户若干元,经调查,种植亩数![]() (亩)与补贴数额
(亩)与补贴数额![]() (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:
| 补贴数额(元) | 10 | 20 | …… |
| 种植亩数(亩) | 160 | 240 | …… |
随着补贴数额![]() 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益![]() (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(1)分别求出政府补贴政策实施后,种植亩数 (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益![]() (元)与政府补贴数额
(元)与政府补贴数额![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)要使全县新种植的牡丹总收益![]() (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额 定为多少元?并求出总收益
定为多少元?并求出总收益 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,为了发展旅游业,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”.已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍.这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元.求混种牡丹的土地有多少亩?(结果精确到个位)(参考数据:![]() )
)
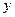 (亩)与补贴数额
(亩)与补贴数额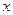 (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:| 补贴数额(元) | 10 | 20 | …… |
| 种植亩数(亩) | 160 | 240 | …… |
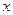 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益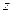 (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.(1)分别求出政府补贴政策实施后,种植亩数
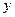 (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益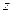 (元)与政府补贴数额
(元)与政府补贴数额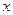 (元)之间的函数关系式;
(元)之间的函数关系式;(2)要使全县新种植的牡丹总收益
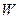 (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额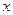 定为多少元?并求出总收益
定为多少元?并求出总收益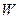 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数)(3)在(2)问中取得最大总收益的情况下,为了发展旅游业,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”.已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍.这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元.求混种牡丹的土地有多少亩?(结果精确到个位)(参考数据:
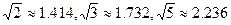 )
) | 补贴数额(元) | 10 | 20 | … |
| 种植亩数(亩) | 160 | 240 | … |
(1)分别求出政府补贴政策实施后,种植亩数y(亩)、每亩牡丹的收益z(元)与政府补贴数额x(元)之间的函数关系式;
(2)要使全县新种植的牡丹总收益W(元)最大,又要从政府的角度出发,政府应将每亩补贴数额x定为多少元?并求出总收益W的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,为了发展旅游业,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”.已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍.这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元.求混种牡丹的土地有多少亩?(结果精确到个位)(参考数据:
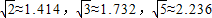 )
)重庆市垫江县具有2000多年的牡丹种植历史.每年3月下旬至4月上旬,主要分布在该县太平镇、澄溪镇明月山一带的牡丹迎春怒放,美不胜收.由于牡丹之根———丹皮是重要中药材,目前已种植有60多个品种2万余亩牡丹的垫江,因此成为我国丹皮出口基地,获得“丹皮之乡”的美誉。为了提高农户收入,该县决定在现有基础上开荒种植牡丹并实行政府补贴,规定每新种植一亩牡丹一次性补贴农户若干元,经调查,种植亩数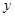 (亩)与补贴数额
(亩)与补贴数额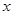 (元)之间成一次函数关系,且补贴与种植情况如下表:
(元)之间成一次函数关系,且补贴与种植情况如下表:
|
补贴数额(元) |
10 |
20 |
…… |
|
种植亩数(亩) |
160 |
240 |
…… |
随着补贴数额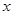 的不断增大,种植规模也不断增加,但每亩牡丹的收益
的不断增大,种植规模也不断增加,但每亩牡丹的收益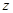 (元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元.
(1)分别求出政府补贴政策实施后,种植亩数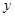 (亩)、每亩牡丹的收益
(亩)、每亩牡丹的收益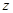 (元)与政府补贴数额
(元)与政府补贴数额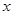 (元)之间的函数关系式;
(元)之间的函数关系式;
(2)要使全县新种植的牡丹总收益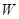 (元)最大,又要从政府的角度出发,政府应将每亩补贴数额
(元)最大,又要从政府的角度出发,政府应将每亩补贴数额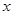 定为多少元?并求出总收益
定为多少元?并求出总收益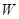 的最大值和此时种植亩数;(总收益=每亩收益×亩数)
的最大值和此时种植亩数;(总收益=每亩收益×亩数)
(3)在(2)问中取得最大总收益的情况下,为了发展旅游业,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植刚由国际牡丹园培育出的“黑桃皇后”.已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍.这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元.求混种牡丹的土地有多少亩?(结果精确到个位)(参考数据: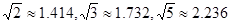 )
)