题目内容
如图，正比例函数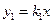
与反比例函数
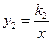相交于A、B点．已知点A的坐标为A（4，n），BD⊥x轴于点D，且
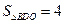．过点A的一次函数
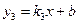与反比例函数的图象交于另一点C，与x轴交于点E（5，0）．
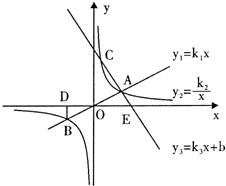
（1）求正比例函数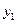
、反比例函数
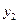和一次函数
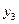的解析式；
（2）结合图象，求出当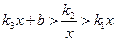
时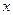
的取值范围．
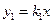与反比例函数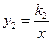相交于A、B点．已知点A的坐标为A（4，n），BD⊥x轴于点D，且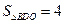．过点A的一次函数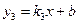与反比例函数的图象交于另一点C，与x轴交于点E（5，0）．（1）求正比例函数
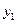、反比例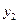函数和一次函数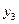的解析式；（2）结合图象，求出当
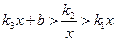时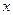的取值范围．解：（1）∵S△BDO=4．
∴k2=2×4=8，
∴反比例函数解析式；y2=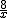
，
∵点A（4，n）在反比例函数图象上，
∴4n=8，
n=2，
∴A点坐标是（4，2），
∵A点（4，2）在正比例函数y1=k1x图象上，
∴2=k1•4，
k1=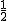
，
∴正比例函数解析式是：y1=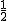x，
∵一次函数y3=k3x+b过点A（4，2），E（5，0），
∴
，
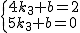解得：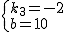
，
∴一次函数解析式为：y3=-
2x+10；
（2）由-2x+10=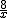解得另一交点C的坐标是（1，8），
点A（4，2）和点D关于原点中心对称，
∴D（-4，-2），
∴由观察可得x的取值范围是：x＜-4，或1＜x＜4．
∴k2=2×4=8，
∴反比例函数解析式；y2=
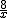，∵点A（4，n）在反比例函数图象上，
∴4n=8，
n=2，
∴A点坐标是（4，2），
∵A点（4，2）在正比例函数y1=k1x图象上，
∴2=k1•4，
k1=
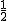，∴正比例函数解析式是：y1=
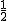x，∵一次函数y3=k3x+b过点A（4，2），E（5，0），
∴
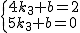，解得：
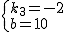，∴一次函数解析式为：y3=-
2x+10；（2）由-2x+10=
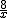解得另一交点C的坐标是（1，8），点A（4，2）和点D关于原点中心对称，
∴D（-4，-2），
∴由观察可得x的取值范围是：x＜-4，或1＜x＜4．
略
练习册系列答案
相关题目
与一次函数y=bx+c的图像在同一坐标系内的图像大致是
，3）若把菱形OCAB绕点A逆时针旋转90°，则点P的对应点P′的坐标是__________。
轴对称，则点B的坐标为
与y=x﹣1的图象的交点坐标为（a，b），则
﹣
的值为 __________________
中,自变量
的取值范围是 
的自变量x的取值范围在数轴上表示为（ ）
