题目内容
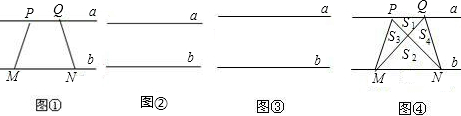
已知四边形S1的两条对角线相等,但不垂直,顺次连接S1各边中点得四边形S2,顺次连接S2各边中点得四边形S3,以此类推,则S2006为( )
分析:顺次连接对角线相等的四边形各边的中点所得的四边形是菱形,顺次连接对角线互相垂直的四边形各边的中点所得的四边形是矩形.
解答:解:∵四边形S1的两条对角线相等,但不垂直,
∴根据三角形的中位线定理,顺次连接S1各边中点所得的四边形的四边相等,则所得的四边形是菱形但不是矩形,
∵菱形S2的对角线互相垂直平分,
∴顺次连接S2各边中点得矩形S3,
又矩形S3的对角线相等,但不垂直,
∴顺次连接S3各边中点得菱形S4,
…
可以发现四边形Sn,当n为奇数(n>1)时,为矩形;当n为偶数时,为菱形但不是矩形.
则S2006为菱形但不是矩形.
故选B.
∴根据三角形的中位线定理,顺次连接S1各边中点所得的四边形的四边相等,则所得的四边形是菱形但不是矩形,
∵菱形S2的对角线互相垂直平分,
∴顺次连接S2各边中点得矩形S3,
又矩形S3的对角线相等,但不垂直,
∴顺次连接S3各边中点得菱形S4,
…
可以发现四边形Sn,当n为奇数(n>1)时,为矩形;当n为偶数时,为菱形但不是矩形.
则S2006为菱形但不是矩形.
故选B.
点评:本题考查了三角形的中位线定理,难度中等,需要掌握三角形的中位线平行于第三边,并且等于第三边的一半,另外要熟练掌握菱形和矩形的判定.

练习册系列答案
相关题目