题目内容
两条平行线a、b被第三条直线c所截得的同旁内角的平分线的交点到直线c的距离是2cm,则a、b之间的距离是
- A.3cm
- B.4cm
- C.5cm
- D.6cm
B
分析:作出图形,过角平分线的交点P作EF⊥b,可以证明EF⊥a,所以EF的长度就是两平行线a、b之间的距离,然后根据角平分线上的点到角的两边的距离相等求出PE=PF=PD,从而问题得解.
解答: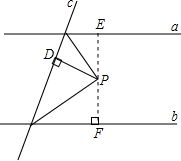 解:如图,过点P作EF⊥b,
解:如图,过点P作EF⊥b,
∵a∥b,
∴EF⊥a,
∴EF就是a、b之间的距离,
∵P到直线c的距离是2,即PD=2cm,点P是同旁内角的平分线的交点,
∴PE=PD,PF=PD,(角平分线上的点到角的两边的距离相等),
∴EF=PE+PF=2+2=4cm.
故选B+.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,平行线的性质,根据题意作出图形从而构造出两直线之间的距离是解题的关键.
分析:作出图形,过角平分线的交点P作EF⊥b,可以证明EF⊥a,所以EF的长度就是两平行线a、b之间的距离,然后根据角平分线上的点到角的两边的距离相等求出PE=PF=PD,从而问题得解.
解答:
 解:如图,过点P作EF⊥b,
解:如图,过点P作EF⊥b,∵a∥b,
∴EF⊥a,
∴EF就是a、b之间的距离,
∵P到直线c的距离是2,即PD=2cm,点P是同旁内角的平分线的交点,
∴PE=PD,PF=PD,(角平分线上的点到角的两边的距离相等),
∴EF=PE+PF=2+2=4cm.
故选B+.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,平行线的性质,根据题意作出图形从而构造出两直线之间的距离是解题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
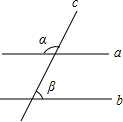 如图,两条平行线a、b被第三条直线c所截,∠а=120°,则cosβ=
如图,两条平行线a、b被第三条直线c所截,∠а=120°,则cosβ=