Question

体育课上，老师用绳子围成一个周长为30米的游戏场地，围成的场地是如图所示的矩形ABCD．设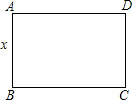边AB的长为x（单位：米），矩形ABCD的面积为S（单位：平方米）．
（1）求S与x之间的函数关系式（不要求写出自变量x的取值范围）；
（2）若矩形ABCD的面积为50平方米，且AB＜AD，请求出此时AB的长．

Answer 1

分析：（1）根据长方形的面积公式求出S与x之间的函数关系式．
（2）根据矩形ABCD的面积为50平方米，即S=50，即可列出一元二次方程求解．

解答：解：（1）根据题意AD=

30-2x

2

=15-x，
S=x（15-x）=-x²+15x

（2）当S=50时，-x²+15x=50，
整理得x²-15x+50=0
解得x₁=5，x₂=10
当AB=5米时，AD=10米；
当AB=10米时，AD=5米
∵AB＜AD
∴AB=5米
答：当矩形ABCD的面积为50平方米且AB＜AD时，AB的长为5米．

点评：对于长方形的面积公式要熟记．注意本题AB＜AD，因此可根据这个条件舍去不合题意的解．