题目内容
(2004•乌鲁木齐)一个小孩荡秋千,如图所示,秋千链子的长OA为2.5米,当秋千向两边摆动时,摆角∠BOD恰好是60°,并且两边摆动角度相同,求:(1)秋千摆至最高位置时与最低位置时的高度之差;
(2)秋千从B点摆动至D点所走过的路程.(结果都精确到0.01)

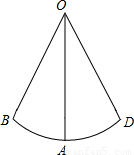
【答案】分析:(1)连接BD交OA于C点,则AC即为所求,OD=OA,先由OD及∠AOD的余弦值求得OC的长,则AC即可求出.
(2)由OD及∠BOD的角利用弧长公式求得秋千从B点摆动至D点所走过的路程.
解答:解:(1)连接BD交OA于C点,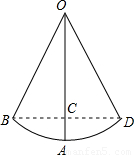
∴∠BOA=∠DOA=30°,OA⊥BD,
在Rt△OCD中:cos30°=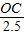 ,
,
∴OC=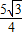 米.
米.
OA-OC= -
-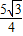 ≈0.33米;
≈0.33米;
(2)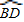 =
=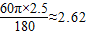 米.
米.
答:它们的高度之差约为0.33米,秋千从B点摆动至D点所走过的路程约为2.62米.
点评:本题考查了解直角三角形的实际应用及弧长的求法.
(2)由OD及∠BOD的角利用弧长公式求得秋千从B点摆动至D点所走过的路程.
解答:解:(1)连接BD交OA于C点,

∴∠BOA=∠DOA=30°,OA⊥BD,
在Rt△OCD中:cos30°=
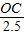 ,
,∴OC=
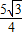 米.
米.OA-OC=
 -
-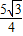 ≈0.33米;
≈0.33米;(2)
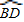 =
=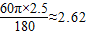 米.
米.答:它们的高度之差约为0.33米,秋千从B点摆动至D点所走过的路程约为2.62米.
点评:本题考查了解直角三角形的实际应用及弧长的求法.

练习册系列答案
相关题目
 的自变量x的取值范围是( )
的自变量x的取值范围是( ) 时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.
时,(3)小题中平行四边形的面积是否有最大值?若有,请求出;若无,请说明理由.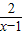 的自变量x的取值范围是( )
的自变量x的取值范围是( ) 的自变量x的取值范围是( )
的自变量x的取值范围是( ) 图象上,若PQ平行于y轴,求出点Q的坐标.
图象上,若PQ平行于y轴,求出点Q的坐标.