题目内容
【题目】如图①，在长方形ABCD中，E点在AD上，且∠ABE＝40°，分别以BE、CE为折痕进行折叠并压平，如图②．若图②中∠BCE＝n°，则∠AED的度数为_________°．（用含n的代数式表示）
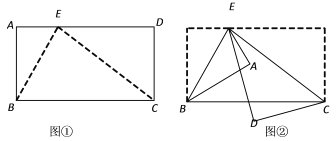
【答案】2n-80
【解析】由题意得：∵BE=2AE=2A′E，∠A=∠A′=90°，即可得△ABE、△A′BE为直角三角形，然后可求得∠AED′的度数，又由∠BCE=n°，即可求得∠AED的度数．
解：根据题意得：∵∠A=∠A/=90°，△A′BE为直角三角形，
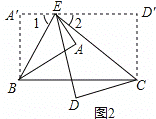
∴∠1=∠AEB=50°，
∵∠BCE=n°
∴∠AED/=180°-∠1-∠AEB=180°-50°-50°=80°，
∴∠DED/=∠AED+∠AED/=2n°，
∴∠AED=∠DED/–∠AED/=2=2n– 80°，
故答案为：2n– 80°.
“点睛”此题考查了折叠的性质、矩形的性质以及含30°角的直角三角形的性质．此题难度适中，注意数形结合思想的应用，注意折叠中的对应关系．
练习册系列答案
相关题目
