题目内容
如图所示,图象反映的是:张阳从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示张阳离家的距离.根据图象回答下列问题:

(1)体育场离张阳家_________千米;
(2)体育场离文具店_________千米;张阳在文具店逗留了_____分钟;
(3)请计算:张阳从文具店到家的平均速度约是每小时多少千米?
(1)点B的坐标是(3,4)(2)当t=1.5秒或t=4.5秒时,MN=![]() AC.
AC.
(3) 抛物线S=- ![]() t2+4 t,当t=3时,S有最大值6.
t2+4 t,当t=3时,S有最大值6.
【解析】
试题分析:解:(1)点B的坐标是(3,4) (2)当t=1.5秒或t=4.5秒时,MN=![]() AC(3) 当t=3时,S有最大值6.
AC(3) 当t=3时,S有最大值6.

(2)当0<t≤3时,(图1)
∵MN∥AC,且MN=![]() AC,
AC,
∴M是OA的中点.
∴t=1.5秒.

当3<t<6时,(图2)
设直线m与x轴交点为D,
∵MN∥AC且MN=![]() AC,
AC,
∴M为AB的中点.
可证:△AMD≌△BMN.
∴BN=AD=t-3.
∴△BMN~△BAC.
∴![]()
∴![]() =
=![]() .
.
∴t=4.5秒.
当t=1.5秒或t=4.5秒时,MN=![]() AC.
AC.
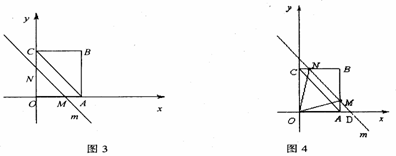
(3)当0<t≤3时,OM=t.(图3)
由△OMN~△OAC,得![]() ,
,
∴ON=![]() t,S=
t,S=![]() t2.
t2.
当3< t<6时,(图4)
∵OD= t,∴AD= t-3.
易知四边形ADNC是平行四边形,∴CN=AD=t-3.BN=6-t.
由△BMN~△BAC,可得BM=![]() BN=8-
BN=8-![]() t,∴AM=-4+
t,∴AM=-4+![]() t.
t.
S=矩形OABC的面积-Rt△OAM的面积-Rt△MBN的面积-Rt△NCO的面积
=12-![]() (-4+
(-4+![]() t) -
t) - ![]() ×(8-
×(8-![]() t)(6-t) -
t)(6-t) - ![]() (t-3)
(t-3)
=-![]() t2+4t.
t2+4t.
当0<t≤3时,
∵抛物线S=![]() t2的开口向上,在对称轴t =0的右边,S随t的增大而增大,
t2的开口向上,在对称轴t =0的右边,S随t的增大而增大,
∴当t =3时,S可取到最大值![]() ×32=6.
×32=6.
当3<t<6时,
∵抛物线S=- ![]() t2+4 t的开口向下,它的顶点是(3,6),
t2+4 t的开口向下,它的顶点是(3,6),
∴S<6. 综上,当t=3时,S有最大值6.
考点:二次函数的综合题型
点评:本题是二次函数的综合题型,其中涉及到的知识点有矩形的性质、三角形中位线定理、全等三角形及相似三角形的判定和性质、二次函数的应用等.在求有关动点问题时要注意分析题意分情况讨论结果.

 金钥匙试卷系列答案
金钥匙试卷系列答案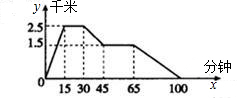 如图所示,图象反映的是:小明从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,其中x表示时间,y表示小明离家的距离.根据图象回答下列问题:
如图所示,图象反映的是:小明从家里跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,其中x表示时间,y表示小明离家的距离.根据图象回答下列问题:

