题目内容
 如图,小明设计了一个电子游戏,一个跳蚤从横坐标为t(t>0)的P1点开始按点的横坐标依次增加1的规律,在抛物线y=ax2上向右跳动,得到P1,P2,P3,这时△P1P2P3面积为( )
如图,小明设计了一个电子游戏,一个跳蚤从横坐标为t(t>0)的P1点开始按点的横坐标依次增加1的规律,在抛物线y=ax2上向右跳动,得到P1,P2,P3,这时△P1P2P3面积为( )| A、a | B、2a | C、3a | D、4a |
分析:首先根据P1的横坐标,表示出P2、P3的横坐标,根据抛物线的解析式,可求得P1、P2、P3的纵坐标,分别过P1、P2、P3作x轴的垂线,然后将△P1P2P3的面积转化为大梯形的面积减去两个小梯形的面积,进而可判断出△P1P2P3的面积.
解答: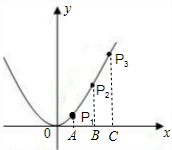 解:作P1A⊥x轴,P2B⊥x轴,P3C⊥x轴,垂足分别为A,B,C.
解:作P1A⊥x轴,P2B⊥x轴,P3C⊥x轴,垂足分别为A,B,C.
由题意得:A(t,0),B(t+1,0),C(t+2,0),
P1(t,at2),P2(t+1,at2+2at+a),P3(t+2,at2+4at+4a);
则:△P1P2P3的面积S=S梯形P1ACP3-S梯形P1ABP2-S梯形P2BCP3=
(at2+at2+4at+4a)×2-
(at2+at2+2at+a)-
(at2+2at+a+at2+4at+4a)
=a.
故选A.
 解:作P1A⊥x轴,P2B⊥x轴,P3C⊥x轴,垂足分别为A,B,C.
解:作P1A⊥x轴,P2B⊥x轴,P3C⊥x轴,垂足分别为A,B,C.由题意得:A(t,0),B(t+1,0),C(t+2,0),
P1(t,at2),P2(t+1,at2+2at+a),P3(t+2,at2+4at+4a);
则:△P1P2P3的面积S=S梯形P1ACP3-S梯形P1ABP2-S梯形P2BCP3=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=a.
故选A.
点评:此题主要考查了函数图象上点的坐标意义,图形面积的求法等知识点.不规则图形的面积可转化为规则图形面积的和差来解.

练习册系列答案
相关题目
 (2013•玄武区一模)小明设计了一个“简易量角器”:如图,在△ABC中,∠C=90°,∠A=30°,CA=30cm,在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°.
(2013•玄武区一模)小明设计了一个“简易量角器”:如图,在△ABC中,∠C=90°,∠A=30°,CA=30cm,在AB边上有一系列点P1,P2,P3…P8,使得∠P1CA=10°,∠P2CA=20°,∠P3CA=30°,…∠P8CA=80°. 如图,小明设计了一个电子游戏,一个跳蚤从横坐标为t(t>0)的P1点开始按点的横坐标依次增加1的规律,在抛物线y=ax2上向右跳动,得到P1,P2,P3,这时△P1P2P3面积为
如图,小明设计了一个电子游戏,一个跳蚤从横坐标为t(t>0)的P1点开始按点的横坐标依次增加1的规律,在抛物线y=ax2上向右跳动,得到P1,P2,P3,这时△P1P2P3面积为
