Question

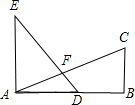如图，已知EA⊥AB，BC∥EA，EA=AB=2BC，D为AB的中点，那么下列式子不能成立的是

1. A.
   DE=AC
2. B.
   DE⊥AC
3. C.
   ∠CAB=30°
4. D.
   ∠EAF=∠ADF

Answer 1

C
分析：已知EA=AB=2BC，且D是AB中点，那么AD=BC，进而可证得△AED、△BAC全等，可根据这个条件进行判断．
解答：∵EA=AB=2BC，AB=2AD，
∴AD=BC；
又∵EA⊥AB，BC∥EA，即∠EAD=∠B=90°，
∴Rt△EAD≌Rt△ABC，
∴DE=AC；
又∠EAF、∠ADF同为∠FAD的余角，
∴∠EAF=∠ADE；
故A、B、D的结论都正确；
Rt△CAB中，AB=2BC，显然sin∠CAB≠，所以∠CAB≠30°，因此C的结论是错误的；
故选C．
点评：此题涉及到直角三角形全等的判定和性质、平行线的性质、同角的余角相等等知识点，难度适中．